Dyjtyuk

用球座標(r, θ, ϕ)displaystyle (r, theta , phi )來表示一個點的位置

在數學裏，球座標系（Spherical coordinate system）是一種利用球座標(r, θ, ϕ)displaystyle (r, theta , phi )表示一個點p在三維空間的位置的三維正交座標系。

右圖顯示了球座標的幾何意義：原點與點P之間的徑向距離rdisplaystyle r，原點到點P的連線與正z-軸之間的天頂角θdisplaystyle theta ，以及原點到點P的連線，在xy-平面的投影線，與正x-軸之間的方位角ϕdisplaystyle phi 。

標記

在學術界內，關於球座標系的標記有好幾個不同的約定。按照國際標準化組織建立的約定（ISO 31-11），徑向距離、天頂角、方位角，分別標記為(r, θ, ϕ)displaystyle (r, theta , phi )。這種標記在世界各地有許多使用者。通常，物理界的學者也採用這種標記。而在數學界，天頂角與方位角的標記正好相反：ϕdisplaystyle phi 被用來代表天頂角，θdisplaystyle theta 被用來代表方位角。數學界的球座標標記是(ρ, ϕ, θ)displaystyle (rho , phi , theta )。這種標記的優點是較廣的相容性；在二維極座標系與三維圓柱座標系裏，ρdisplaystyle rho 都同樣地代表徑向距離，θdisplaystyle theta 也都同樣地代表方位角。本條目採用的是物理標記約定。

定義

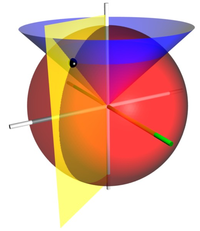
球座標系的幾個座標曲面。紅色圓球面的r=2displaystyle r=2。藍色圓錐面的θ=45∘displaystyle theta =45^circ 。黃色半平面的ϕ=−60∘displaystyle phi =-60^circ （黃色半平面與xz-半平面之間的二面角角度是|ϕ|）。z-軸是垂直的，以白色表示。x-軸以綠色表示。三個座標曲面相交於點P（以黑色的圓球表示）。直角座標大約為(0.707,−1.225,1.414)displaystyle (0.707,-1.225,1.414)。

假設P點在三維空間的位置的三個座標是(r, θ, ϕ)displaystyle (r, theta , phi )。那麼，0 ≤ r是從原點到P點的距離，0 ≤ θ ≤ π是從原點到P點的連線與正z-軸的夾角，0 ≤ φ < 2π是從原點到P點的連線在xy-平面的投影線，與正x-軸的夾角。

這裏，θdisplaystyle theta 代表天頂角，ϕdisplaystyle phi 代表方位角。當 r=0displaystyle r=0時，θdisplaystyle theta 與ϕdisplaystyle phi 都一起失去意義。當θ=0displaystyle theta =0或θ=πdisplaystyle theta =pi 時，ϕdisplaystyle phi 失去意義。

如想要用球座標，找出點P在空間的地點，可按照以下步驟：

1. 從原點往正z-軸移動rdisplaystyle r單位，


2. 用右手定則，大拇指往y-軸指，x-軸與z-軸朝其他手指的指向旋轉θdisplaystyle theta 角值，


3. 用右手定則，大拇指往z-軸指，x-軸與y-軸朝其他手指的指向旋轉ϕdisplaystyle phi 角值。

座標系變換

三維空間裏，有各種各樣的座標系。球座標系只是其中一種。球座標系與其他座標系的變換需要用到特別的方程式。

直角座標系

使用以下等式，可從直角座標變換為球座標：

r=x2+y2+z2displaystyle r=sqrt x^2+y^2+z^2，

θ=arccos⁡(zr)=arcsin⁡(x2+y2r)=arctan⁡(x2+y2z)displaystyle theta =arccos left(frac zrright)=arcsin left(frac sqrt x^2+y^2rright)=arctan left(frac sqrt x^2+y^2zright)，

ϕ=arccos⁡(xrsin⁡θ)=arcsin⁡(yrsin⁡θ)=arctan⁡(yx)displaystyle phi =arccos left(frac xrsin theta right)=arcsin left(frac yrsin theta right)=arctan left(frac yxright)。

計算 ϕdisplaystyle phi 時：

1. 必須依照 (x, y)displaystyle (x, y) 所處的象限來計算正確的反正切值。

2. 當 x=0displaystyle x=0 時，判斷 ydisplaystyle y 的值：

若 y>0displaystyle y>0，則 ϕ=π2displaystyle phi =frac pi 2，

若 y<0displaystyle y<0，則 ϕ=−π2displaystyle phi =-frac pi 2，

若 y=0displaystyle y=0，則 ϕdisplaystyle phi 為未定值 ( 因為 00displaystyle frac 00 為未定式 )。

反過來，也可從球座標變換為直角座標：

x=rsin⁡θcos⁡ϕdisplaystyle x=rsin theta cos phi ，

y=rsin⁡θsin⁡ϕdisplaystyle y=rsin theta sin phi ，

z=rcos⁡θdisplaystyle z=rcos theta 。

地理座標系

地理座標系是球座標系的第二個版本。地理座標標记为(ρ, λ, δ)displaystyle (rho , lambda , delta )，其中ρdisplaystyle rho ,表示径向距离，λdisplaystyle lambda 表示方位角，δdisplaystyle delta 表示高度角。它主要是用在地理學。通常在地理學裏，ρdisplaystyle rho ,會被用來表示高度，或者完全不被使用。

緯度的定義域是0∘≤δ≤90∘displaystyle 0^circ leq delta leq 90^circ ，南緯或北緯。使用以下方程式，可從緯度δdisplaystyle delta 變換為天頂角：

1. 
   θ≤90∘displaystyle theta leq 90^circ ：北緯，δ=90∘−θdisplaystyle delta =90^circ -theta ，


2. 
   θ≥90∘displaystyle theta geq 90^circ ：南緯，δ=θ−90∘displaystyle delta =theta -90^circ 。

經度λdisplaystyle lambda 的定義域是−180∘≤λ≤180∘displaystyle -180^circ leq lambda leq 180^circ 。設定經過倫敦格林維治天文台的子午線為經度0∘displaystyle 0^circ ，往東或往西λdisplaystyle lambda 度。使用以下方程式，可從經度變換為方位角

1. 
   ϕ≤180∘displaystyle phi leq 180^circ ：往東，λ=ϕdisplaystyle lambda =phi ，


2. 
   ϕ≥180∘displaystyle phi geq 180^circ ：往西，λ=ϕ−360∘displaystyle lambda =phi -360^circ 。

圓柱座標系

用圓柱座標來表示一個點的位置

圓柱座標系是極座標系在三維空間往z-軸的延伸。zdisplaystyle z座標用來表示高度。使用以下方程式，可以從球座標變換為圓柱座標(ρ, ϕ, z)displaystyle (rho , phi , z)：

r=ρ2+z2displaystyle r=sqrt rho ^2+z^2、

θ=arctan⁡ρzdisplaystyle theta =arctan frac rho z、

ϕ=ϕdisplaystyle phi =phi 。

反過來，可以從圓柱座標變換為球座標：

ρ=rsin⁡θdisplaystyle rho =rsin theta 、

ϕ=ϕdisplaystyle phi =phi 、

z=rcos⁡θdisplaystyle z=rcos theta 。

標度因子

球座標系的標度因子分別為：

hr=1displaystyle h_r=1、

hθ=rdisplaystyle h_theta =r、

hϕ=rsin⁡θdisplaystyle h_phi =rsin theta 。

無窮小體積元素是

dV=r2sin⁡θdrdθdϕdisplaystyle dV=r^2sin theta ,dr,dtheta ,dphi 。

拉普拉斯算子是

∇2Φ=1r2∂∂r(r2∂Φ∂r)+1r2sin⁡θ∂∂θ(sin⁡θ∂Φ∂θ)+1r2sin2⁡θ∂2Φ∂ϕ2displaystyle nabla ^2Phi =1 over r^2partial over partial r!left(r^2partial Phi over partial rright)!+!1 over r^2!sin theta partial over partial theta !left(sin theta partial Phi over partial theta right)!+!1 over r^2!sin ^2theta partial ^2Phi over partial phi ^2。

其它微分算子，像∇⋅Fdisplaystyle nabla cdot mathbf F 、∇×Fdisplaystyle nabla times mathbf F ，都可以用(r, θ, ϕ)displaystyle (r, theta , phi )座標表示，只要將標度因子代入在正交座標系條目內對應的一般公式。

球坐标系下的积分和微分公式

假定θdisplaystyle theta 是從原點到P點的連線與正z-軸的夾角

• 线元素是一个从(r,θ,ϕ)displaystyle (r,theta ,phi )到(r+dr,θ+dθ,ϕ+dϕ)displaystyle (r+mathrm d r,,theta +mathrm d theta ,,phi +mathrm d phi )的无穷小位移，表示为公式：

dr=drr^+rdθθ^+rsin⁡θdϕϕ^displaystyle mathrm d mathbf r =mathrm d r,boldsymbol hat r+r,mathrm d theta ,boldsymbol hat theta +rsin theta mathrm d phi ,mathbf boldsymbol hat phi ；

其中的r^,θ^,ϕ^displaystyle boldsymbol hat r,boldsymbol hat theta ,boldsymbol hat phi 是在r,θ,ϕdisplaystyle r,theta ,phi 的各自的增加的方向上的单位矢量。

• 面积元素1：在球面上，固定半径，天顶角从θdisplaystyle theta 到θ+dθdisplaystyle theta +mathrm d theta ，方位角从ϕdisplaystyle phi 到ϕ+dϕdisplaystyle phi +mathrm d phi 变化，公式为：

dSr=r2sin⁡θdθdϕdisplaystyle mathrm d S_r=r^2sin theta ,mathrm d theta ,mathrm d phi 。

• 面积元素2：固定天顶角θdisplaystyle theta ，其他两个变量变化，則公式为：

dSθ=rsin⁡θdrdϕdisplaystyle mathrm d S_theta =r,sin theta ,mathrm d r,mathrm d phi 。

• 面积元素3：固定方位角ϕdisplaystyle phi ，其他两个变量变化，則公式为：

dSϕ=rdrdθdisplaystyle mathrm d S_phi =r,mathrm d r,mathrm d theta 。

• 体积元素，徑向座標从rdisplaystyle r到r+drdisplaystyle r+mathrm d r，天顶角从θdisplaystyle theta 到θ+dθdisplaystyle theta +mathrm d theta ，并且方位角从ϕdisplaystyle phi 到ϕ+dϕdisplaystyle phi +mathrm d phi 的公式为：

dV=r2sin⁡θdrdθdϕdisplaystyle mathrm d V=r^2sin theta ,mathrm d r,mathrm d theta ,mathrm d phi 。

• 
  梯度公式：

∇f=∂f∂rr^+1r∂f∂θθ^+1rsin⁡θ∂f∂ϕϕ^displaystyle nabla f=partial f over partial rboldsymbol hat r+1 over rpartial f over partial theta boldsymbol hat theta +1 over rsin theta partial f over partial phi boldsymbol hat phi 。

• 
  散度公式：

∇⋅A=1r2∂∂r(r2Ar)+1rsin⁡θ∂∂θ(sin⁡θAθ)+1rsin⁡θ∂Aϕ∂ϕdisplaystyle nabla cdot mathbf A =frac 1r^2partial over partial rleft(r^2A_rright)+frac 1rsin theta partial over partial theta left(sin theta A_theta right)+frac 1rsin theta partial A_phi over partial phi 。

• 
  旋度公式：

∇×A=1rsin⁡θ(∂∂θ(Aϕsin⁡θ)−∂Aθ∂ϕ)r^+1r(1sin⁡θ∂Ar∂ϕ−∂∂r(rAϕ))θ^+1r(∂∂r(rAθ)−∂Ar∂θ)ϕ^displaystyle nabla times mathbf A =displaystyle 1 over rsin theta left(partial over partial theta left(A_phi sin theta right)-partial A_theta over partial phi right)boldsymbol hat r+displaystyle 1 over rleft(1 over sin theta partial A_r over partial phi -partial over partial rleft(rA_phi right)right)boldsymbol hat theta +displaystyle 1 over rleft(partial over partial rleft(rA_theta right)-partial A_r over partial theta right)boldsymbol hat phi 。

• 
  拉普拉斯算子是

∇2f=1r2∂∂r(r2∂f∂r)+1r2sin⁡θ∂∂θ(sin⁡θ∂f∂θ)+1r2sin2⁡θ∂2f∂ϕ2displaystyle nabla ^2f=1 over r^2partial over partial r!left(r^2partial f over partial rright)!+!1 over r^2!sin theta partial over partial theta !left(sin theta partial f over partial theta right)!+!1 over r^2!sin ^2theta partial ^2f over partial phi ^2。

應用

地理座標系用兩個角值，緯度與經度，來表示地球表面的地點。正如二維直角座標系專精在平面上，二維球座標系可以很簡易的設定圓球表面上的點的位置。在這裏，我們認定這圓球是個單位圓球；其半徑是1。通常我們可以忽略這圓球的半徑。在解析旋轉矩陣問題上，這方法是非常有用的。

球座標系適用於分析一個對稱於點的系統。舉例而言，一個圓球，其直角座標方程式為x2+y2+z2=c2displaystyle x^2+y^2+z^2=c^2，可以簡易的用球座標系ρ=cdisplaystyle rho =c來表示。

當求解三重積分時，如果定義域為圓球，則面積元素是

dS=r2sin⁡θdθdϕdisplaystyle dS=r^2sin theta ,dtheta ,dphi ；

體積元素是

dV=r2sin⁡θdrdθdϕdisplaystyle dV=r^2sin theta ,dr,dtheta ,dphi 。

用來描述與分析擁有球狀對稱性質的物理問題，最自然的座標系，莫非是球座標系。例如，一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式，拉普拉斯方程與亥姆霍茲方程，在球座標裏，都可以成功的使用分離變數法求得解答。這種方程式在角部分的解答，皆呈球諧函數的形式。

球座標的概念，延伸至高維空間，則稱為超球座標 (n-sphere)。

參閱