考克斯特群
在數學中,考克斯特群是一類由空間中對超平面的鏡射生成的群。這類群廣泛出現於數學的各分支中,二面體群與正多胞體的對稱群都是例子;此外,根系對應到的外爾群也是考克斯特群。這類群以數學家哈羅德·斯科特·麥克唐納·考克斯特命名。
目录
1 形式定義
2 性質
3 例子
4 分類
5 文獻
形式定義
所謂考克斯特群,是一個群 Wdisplaystyle W
- ⟨r1,r2,…,rn∣(rirj)mij=1⟩displaystyle leftlangle r_1,r_2,ldots ,r_nmid (r_ir_j)^m_ij=1rightrangle
其中 mij∈N∪∞displaystyle m_ijin mathbb N cup infty 
- 對稱性- mij=mjidisplaystyle m_ij=m_ji
- i≠j⇒mij≥2displaystyle ineq jRightarrow m_ijgeq 2
- mii=1displaystyle m_ii=1
在此 mij=∞displaystyle m_ij=infty 




令這組生成元為 Sdisplaystyle S


性質
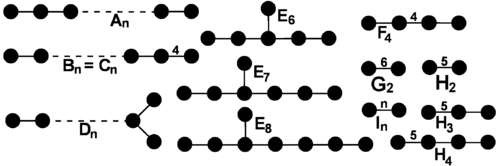
有限考克斯特群的分類
設 (W,S)displaystyle (W,S)






利用 (W,S)displaystyle (W,S)




- ∀s∈S,ℓ(ws)=ℓ(w)±1displaystyle forall sin S,;ell (ws)=ell (w)pm 1
- ℓ(w−1)=ℓ(w)displaystyle ell (w^-1)=ell (w)
例子
對稱群 Sndisplaystyle S_n是考克斯特群。在此可取 Sdisplaystyle S
為置換 (1,2),(2,3),…,(n−1,n)displaystyle (1,2),(2,3),ldots ,(n-1,n)
;關係為 ((k,k+1)(k+1,k+2))3=1displaystyle ((k,k+1)(k+1,k+2))^3=1
。
- 正多胞體的對稱:正多胞體的對稱群是有限考克斯特群。舉例明之:正多邊形的對稱群是二面體群,正 n 維單形的對稱群是前述的 Sn+1displaystyle S_n+1
,又稱為 Andisplaystyle A_n
型的考克斯特群。n 維超正方體的對稱群為 BCndisplaystyle BC_n
。正十二面體與正二十面體的對稱群是 H3displaystyle H_3
。在四維空間中,存在三種特別的正多胞體──正二十四胞體、正一百二十胞體與正六百胞體,其對稱群分別是 F4,H4,H4displaystyle F_4,H_4,H_4
。Dn,E6,E7,E8displaystyle D_n,E_6,E_7,E_8
可以由某些半正多胞體的對稱群得到。
外爾群:每個根系的外爾群都是有限考克斯特群。
仿射外爾群:仿射外爾群是無限群,但帶有一個正則阿貝爾子群,使得對應的商群是個外爾群。
分類
一般而言,兩個群展示的同構與否是無法判定的。然而對考克斯特群則有一個簡單的判準,稱為交換條件。可以透過考克斯特-丹金圖分類有限考克斯特群。圖的構造方式為:
- 每個生成元對應到一個頂點。
- 若 mij≥3displaystyle m_ijgeq 3
,則頂點 ri,rjdisplaystyle r_i,r_j
之間有邊相連。
- 若 mij≥4displaystyle m_ijgeq 4
,則將邊標上 mijdisplaystyle m_ij
。
文獻
- Larry C Grove and Clark T. Benson, Finite Reflection Groups (1985), Graduate texts in mathematics, vol. 99, Springer.
- Paul Garrett, Buildings and Classical Groups (1997), Chapman Hall. ISBN 0-412-06331-X . PostScript 檔案下載 .
- James E. Humphreys, Reflection Groups and Coxeter Groups (1990), Cambridge studies in advanced mathematics, 29.





