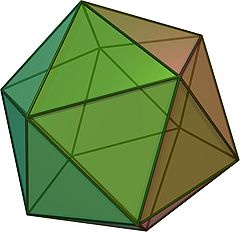
正二十面體

Multi tool use
| 正二十面體 | |
|---|---|
 (按這裡觀看旋轉模型) | |
| 類別 | 正多面体 |
| 面 | 20 |
| 邊 | 30 |
| 頂點 | 12 |
| 歐拉特徵數 | F=20, E=30, V=12 (χ=2) |
| 面的種類 | 正三角形 |
| 面的佈局 | 203 |
| 頂點圖 | 3.3.3.3.3 |
| 施萊夫利符號 | 3,5 and s33displaystyle sbeginBmatrix3\3endBmatrix |
| 對稱群 | 5 |
| 參考索引 | U22, C25, W4 |
| 對偶 | 正十二面體 |
| 二面角 | 138.189685° |
| 特性 | 正凸三角面多面體 |
 3.3.3.3.3 (頂點圖) | |
 (展開圖) | |
正二十面體是一種正多面體,由20個正三角形組成。同時,它也是柏拉圖立體、三角面多面體以及康威多面體。正二十面体是所有五种正多面體面數最多的。
正二十面體有20個面、30個邊和12個頂點,其對偶是正十二面體。它的頂點佈局為3.3.3.3.3或35,在施萊夫利符號中可用3,5來表示。
目录
1 與正十二面體的关系
2 體積與表面積
3 體積與表面積
4 直角坐標系
4.1 球面坐標
4.2 與黃金分割的關係
5 正交投影
6 其它事实
7 通过一系列等夹角线段构造正二十面体
8 半正涂色和子对称群
9 与其它几何图形的关系
10 應用
10.1 在生物學中
11 參考文獻
與正十二面體的关系
在平面上,正多邊形內接到圓時,邊數越多,佔圓面積的百分比就越高;而在三維空間中,這個規則卻不可推廣——當正十二面體和正二十面體內接到一個球時,前者約佔66.4909%,後者僅佔60.5461%。
 正十二面體是正二十面體的對偶多面體。 |
體積與表面積
若有一個邊長為a的正二十面體,則它的外接球(同時過該正二十面體所有頂點的球)的半徑為:
ru=a2φ5=a410+25=asin2π5≈0.9510565163⋅adisplaystyle r_u=frac a2sqrt varphi sqrt 5=frac a4sqrt 10+2sqrt 5=asin frac 2pi 5approx 0.9510565163cdot aA019881
則有內切球(同時和該正二十面體所有面相切的球)的半徑為:
ri=φ2a23=312(3+5)a≈0.7557613141⋅adisplaystyle r_i=frac varphi ^2a2sqrt 3=frac sqrt 312left(3+sqrt 5right)aapprox 0.7557613141cdot aA179294
另外,若有一個球同時過該正二十面體所有邊的中點,那它的半徑為:
rm=aφ2=14(1+5)a=acosπ5≈0.80901699⋅adisplaystyle r_m=frac avarphi 2=frac 14left(1+sqrt 5right)a=acos frac pi 5approx 0.80901699cdot aA019863
其中φ (也稱作τ)為黃金比例。
體積與表面積
若用A表示表面積、V表示體積,而a是正二十面體的邊長,則有:
A=53a2≈8.66025404a2,displaystyle A=5sqrt 3a^2approx 8.66025404a^2,A010527
V=512(3+5)a3≈2.18169499a3.displaystyle V=frac 512(3+sqrt 5)a^3approx 2.18169499a^3.A102208
後者F=20約為正四面體的20倍,因為20面體以外接球球新為中心可以切割出20個四面體,其中的四面體的體積是底面積的三分之一倍,ri是高的 √3a2/4倍。
的外接球體的體積填充率是:
- f=V/(4πru3/3)=20(3+√5)(2√5+10)3/2π≈0.6054613829.displaystyle f=V/(4pi r_u^3/3)=frac 20(3+surd 5)(2surd 5+10)^3/2pi approx 0.6054613829.
直角坐標系
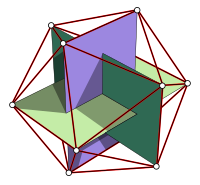
正二十面體的頂點能共同分成五組,每組擁有三個同心、相互垂直的黃金矩形。
在直角坐標系中,一個邊長為二、重心在圓點的正二十面體的坐標分別為:[1]
- (0, ±1, ±φ)
- (±1, ±φ, 0)
- (±φ, 0, ±1)
其中φ = 1 + √5/2是黃金比例(或記為τ)。值得注意的是,這些頂點能共同形成五組,每組擁有三個同心、相互垂直的黃金矩形,其邊形成博羅梅安環,其中,前者是因為正二十面體與黃金比例有密切的關係。
如果原始的二十面體的邊長為1,那麼它的對偶——正十二面體的邊長就是√5 − 1/2,正好是一個黃金比例。

一個由塑膠棒和磁鐵與金屬球連接的正二十面體模型
12條邊的一個正八面體可以被細分在黃金比例,使所得到的頂點可構成一個正二十面體。這首先要使沿著八面體邊的向量連成一個有界的環,再沿著向量的方向以黃金比例作分割。
球面坐標
正二十面體是一個D5d二面體對稱對稱的一個雙五角錐反角柱,且頂點可以定義在球面坐標系上,其中兩個頂點在球的兩極,其餘在緯度±arctan(1/2)的位置。可以發現剩餘的10頂點屬於反棱柱對稱,從一個定點,經度每36°做一次極軸與赤道鏡射,直到回到原始點。
與黃金分割的關係
若以正二十面體的中心為原點,各頂點的坐標分別為(0,±1,±Φ), (±1,±Φ,0), (±Φ,0,±1),在此Φ = √5 − 1/2,即黃金分割數。因此,這些頂點能共同形成五組,每組擁有三個同心、相互垂直的黃金矩形。
正交投影
正二十面体有3种特殊的正交投影,分别正对着一个面、一条棱、一个顶点。
| 正对于 | 面 | 棱 | 顶点 |
|---|---|---|---|
考克斯特平面 | A2 | A3 | H3 |
| 图像 |  |  |  |
| 投影 对称性 | [6] | [2] | [10] |
| 图像 |  面法线 |  棱法线 |  对角线 |
其它事实
- 正二十面体有43,380种不同的展开图。
- 若要将正二十面体的表面涂色而相邻的面的颜色不同,则至少需要3种颜色。
- 内接与同一球的正二十面体和正十二面体,正二十面体所占球的体积(60.54%)要小于正十二面体所占的体积(66.49%)。
通过一系列等夹角线段构造正二十面体
 正二十面体 H3考克斯特平面 |  六维正轴体 D6考克斯特平面 |
| 这个操作可以以几何的观点被看作六维正轴体的12个顶点投影到三维空间。这代表着一个D6到H3考克斯特群的几何折叠: 见这些二维考克斯特平面正交投影,中间投影后重合的两个顶点给出了这个图像中的第三根轴 | |
以下构建正二十面体的方法避免了使用更基础的方法时必要的在数域Q[5]displaystyle mathbb Q [sqrt 5]![displaystyle mathbb Q [sqrt 5]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5691f5e84ebcf23acbd458f90f57c0945549be8c)
正二十面体的存在性依赖于R3displaystyle mathbb R ^3
为了构建这样一个等夹角线系统,我们开始于一个6×6方形矩阵。
- A=(011111101−1−111101−1−11−1101−11−1−110111−1−110).displaystyle A=left(beginarraycrrrrr0&1&1&1&1&1\1&0&1&-1&-1&1\1&1&0&1&-1&-1\1&-1&1&0&1&-1\1&-1&-1&1&0&1\1&1&-1&-1&1&0endarrayright).
通过直接的计算,我们可以得出A2=5I(在这里I是6×6单位矩阵)。这表明矩阵I的特征值是√5和-√5,并且它们的复杂性都是3,因为A是对称的,并且它的迹是0。
矩阵A+5Idisplaystyle scriptstyle A+sqrt 5I








正二十面体另一个直接的构造用到了交错群A5的群表示论方法,它直接利用了正二十面体的等距同构。
半正涂色和子对称群

正二十面体作为扭棱四面体,可以通过旋转正四面体的正三角形面,并在4个顶点处插入新的三角形,在原来的6条棱处插入新的一对三角形来构造
作为正多面体之一,正二十面体拥有较高的对称性,它的所有面在几何上都是相同的,不可区分的。可是我们也可以想象将正二十面体的面“涂上”不同的“颜色”,使它其的不同面拥有不同的“几何意义”,使其拥有不同的次级对称性。正二十面体有三种不同的半正涂色方法,可以按照一个顶点引出的5个面的涂色来标记为11213、11212、11111。正二十面体可以被描述为扭棱正四面体,具有手征性正四面体对称性;它亦可以被描述成交错截顶正八面体,有五角十二面体对称性。这个具有五角十二面体对称的正二十面体也被叫做伪二十面体是五角十二面体的对偶。
| 名称 | 正二十面体 | 交错 截顶八面体 | 扭棱 正四面体 | 正五 双锥反柱体 |
|---|---|---|---|---|
考克斯特-迪肯 | ||||
施莱夫利符号 | 3,5 | h0,13,4 | s3,3 | |
Wythoff符号 | 5 | 3 2 | | 3 3 2 | ||
对称性 | Ih [5,3] (*532) | Th [3+,4] (3*2) | T [3,3]+ (332) | D5d [2+,10] (2*5) |
| 对称群阶 | 60 | 24 | 12 | 10 |
半正涂色 |  (11111) |  (11212) |  (11213) |  (11122)&(22222) |
与其它几何图形的关系
正二十面体是正二十面体家族的一员:
對稱群: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  | |
5,3 | t0,15,3 | t15,3 | t0,13,5 | 3,5 | t0,25,3 | t0,1,25,3 | s5,3 |
| 半正多面体对偶 | |||||||
 |  |  |  |  |  | ||
V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
作为扭棱正四面体和交错截顶正八面体,正二十面体也是正四面体家族和正八面体家族的一员:
对称性: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  | |||
3,3 | t0,13,3 | t13,3 | t1,23,3 | t23,3 | t0,23,3 | t0,1,23,3 | s3,3 |
| 半正多面体对偶 | |||||||
 |  |  |  |  | |||
V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
对称性: [4,3], (*432) | [4,3]+, (432) | [1+,4,3], (*332) | [4,3+], (3*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  | ||||||
4,3 | t0,14,3 | t14,3 | t1,24,3 | 3,4 | t0,24,3 | t0,1,24,3 | s4,3 | h4,3 | h1,24,3 |
| 半正多面体的对偶 | |||||||||
 |  |  |  |  |  |  | |||
V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
正二十面体在拓扑上与其它一系列的正三角形镶嵌3,n和一系列的五阶正镶嵌n,5相关联:
多面体 | 欧式镶嵌 | 双曲镶嵌 | |||||||
|---|---|---|---|---|---|---|---|---|---|
 3,2 |  3,3 |  3,4 |  3,5 |  3,6 |  3,7 |  3,8 |  3,9 | ... |  {3,∞) |
| 球面鑲嵌 | 雙曲面鑲嵌 | |||||||
|---|---|---|---|---|---|---|---|---|
 2,5 |  3,5 |  4,5 |  5,5 |  6,5 |  7,5 |  8,5 | ... |  ∞,5 |
正二十面体和三个星形正多面体有着相同的顶点排布。其中与大十二面体还有相同的棱排布:
| 图像 |  大十二面体 |  小星形十二面体 |  大二十面体 |
|---|---|---|---|
考克斯特-迪肯符号 |
虽然由于正二十面体的二面角太大(约138.189685°>120°),因此正二十面体不可能密铺三维欧几里得空间,但它可以密铺适当的双曲空间,称为三阶正二十面体堆砌,每条棱处有三个正二十面体相交,每个顶点处有12个正二十面体相交,应此顶点图是正十二面体,施莱夫利符号3,5,3,是四个三维双曲空间中的正堆砌之一。
 这里我们用庞加莱圆盘模型上的线架来表示它,中心的正十二面体被涂上了颜色。 |
| 類別 | 正多面體 | 卡塔蘭立體 | |||||
|---|---|---|---|---|---|---|---|
| 種子 |  3,3 |  4,3 |  3,4 |  5,3 |  3,5 |  aC |  aD |
| 倒角 |  cT |  cC |  cO |  cD |  cI |  caC |  caD |
應用

二十面的骰子

電子顯微鏡下觀察的金原子

γ-硼的結構
由於正二十面體非常均勻,且有20個面,因此適合作成骰子。
在生物學中
某些病毒,如疱疹病毒科、諾羅病毒,擁有正二十面體的衣殼。[2][3]在有些細菌中還發現一些具有二十面體形狀的各種細菌的胞器,[4]還有二十面體的殼包住的酶使不穩定的活化複合體得以建構BMC等不同類型的蛋白質。
1904年,恩斯特·海克尔發表了一些放射蟲的種類,包括Circogonia二十面體(Circogonia icosahedra),其骨架的形狀像一個正二十面體。
參考文獻
^ 埃里克·韦斯坦因. Icosahedral group. MathWorld.
^ C. Michael Hogan. 2010. Virus. Encyclopedia of Earth. National Council for Science and the Environment. eds. S. Draggan and C. Cleveland
^ 存档副本. [2005-06-25]. (原始内容存档于2006-03-25).
^ Bobik, T.A., Bacterial Microcompartments, Microbe (Am. Soc. Microbiol.), 2007, 2: 25–31, (原始内容存档于2013-07-29)
.mw-parser-output .refbeginfont-size:90%;margin-bottom:0.5em.mw-parser-output .refbegin-hanging-indents>ullist-style-type:none;margin-left:0.mw-parser-output .refbegin-hanging-indents>ul>li,.mw-parser-output .refbegin-hanging-indents>dl>ddmargin-left:0;padding-left:3.2em;text-indent:-3.2em;list-style:none.mw-parser-output .refbegin-100font-size:100%
Klein, Felix, Lectures on the ikosahedron and the solution of equations of the fifth degree, 1888, Dover edition ISBN 978-0-486-49528-6.
维基共享资源中相关的多媒体资源:正二十面體 |
維基文庫有《大英百科第11版》的條目「Icosahedron」。 |
| 查询維基詞典中的icosahedron。 |
- 埃里克·韦斯坦因. Icosahedron. MathWorld.
- Richard Klitzing, 3D convex uniform polyhedra, x3o5o - ike
Hartley, Michael. Dr Mike's Math Games for Kids.
Webb, Robert. Icosahedron.- The Uniform Polyhedra
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
Interactive Icosahedron model - works right in your web browser
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
Tulane.edu A discussion of viral structure and the icosahedron
Paper Models of Polyhedra Many links
Origami Polyhedra - Models made with Modular Origami- Video of icosahedral mirror sculpture
[1] Principle of virus architecture
Stella: Polyhedron Navigator: Software used to create some of the images on this page.
| ||||||||||||||||||
| ||||||
| ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
XC5 8NEFZRA1SpgAkyzU,Ajax1nRXuoqmkfMmcQwXypRAJ4h,LlRdSAdVRkStfCaIyuM pc3oiuurJTb,5QAu5Z,O syuKeUHIMeW


