移動平均
移動平均(英语:moving average,MA),又稱「移動平均線」簡稱均線,是技術分析中一種分析时间序列數據的工具。最常見的是利用股價、回報或交易量等變數計算出移動平均。
移動平均可撫平短期波動,反映出長期趨勢或周期。數學上,移動平均可視為一種卷积。

台股加權指數技術線圖:
上圖為K線和其移動平均線(SMA,周期:5,10,20,60,120,240);
下圖為成交量和其均量(周期:5,20)。
目录
1 簡單移動平均
2 加權移動平均
3 指數移動平均
4 其他加權
5 內部連結
6 參考文献
7 外部連結
簡單移動平均

比較:圖中同時呈現20日移動平均線-SMA、EMA和WMA。
簡單移動平均(英语:simple moving average,SMA)是某變數之前n個數值的未作加權算術平均。例如,收市價的10日簡單移動平均指之前10日收市價的平均數。若設收市價為p1displaystyle p_1

- SMA=p1+p2+⋯+pnndisplaystyle SMA=p_1+p_2+cdots +p_n over n
當計算連續的數值,一個新的數值加入,同時一個舊數值剔出,所以無需每次都重新逐個數值加起來:
- SMAt1,n=SMAt0,n−p1n+pn+1ndisplaystyle SMA_t1,n=SMA_t0,n-p_1 over n+p_n+1 over n
在技術分析中,不同的市場對常用天數(n值)有不同的需求,例如:某些市場普遍的n值為10日、40日、200日;有些則是5日、10日、20日、60日、120日、240日,視乎分析時期長短而定。投資者冀從移動平均線的圖表中分辨出支持位或阻力位。
加權移動平均
加權移動平均(英语:weighted moving average,WMA)指計算平均值時將個別數據乘以不同數值,在技術分析中,n日WMA的最近期一個數值乘以n、次近的乘以n-1,如此類推,一直到0:
- WMAM=npM+(n−1)pM−1+⋯+2pM−n+2+pM−n+1n+(n−1)+⋯+2+1displaystyle WMA_M=np_M+(n-1)p_M-1+cdots +2p_M-n+2+p_M-n+1 over n+(n-1)+cdots +2+1
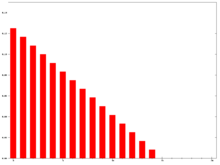
WMA,N=15
由於WMAM+1displaystyle WMA_M+1



- 總和M+1=displaystyle =
總和M+pM+1−pM−n+1displaystyle +p_M+1-p_M-n+1
- 分子M+1=NM+1=displaystyle =N_M+1=
分子M+npM+1−displaystyle +np_M+1-
總和M
- WMAM+1=NM+1n+(n−1)+⋯+2+1displaystyle WMA_M+1=N_M+1 over n+(n-1)+cdots +2+1
留意分母為三角形數,方程式為n(n+1)2displaystyle n(n+1) over 2
右圖顯示出加權是隨日子遠離而遞減,直至遞減至零。
指數移動平均

EMA,N=15
指數移動平均(英语:exponential moving average,EMA或EXMA)是以指數式遞減加權的移動平均。各數值的加權影響力隨時間而指數式遞減,越近期的數據加權影響力越重,但較舊的數據也給予一定的加權值。右圖是一例子。
加權的程度以常數α決定,α數值介乎0至1。α也可用天數N來代表:α=2N+1displaystyle alpha =2 over N+1
設時間t的實際數值為Yt,而時間t的EMA則為St;時間t-1的EMA則為St-1,計算時間t≥2是方程式為:[1]
- St=α×Yt+(1−α)×St−1displaystyle S_t=alpha times Y_t+(1-alpha )times S_t-1
設今日(t1)價格為p,則今日(t1)EMA的方程式為:
- EMAt1=EMAt0+α×(p−EMAt0)displaystyle textEMA_t1=textEMA_t0+alpha times (p-textEMA_t0)
將EMAt0displaystyle textEMA_t0
- EMA=p1+(1−α)p2+(1−α)2p3+(1−α)3p4+⋯1+(1−α)+(1−α)2+(1−α)3+⋯displaystyle textEMA=p_1+(1-alpha )p_2+(1-alpha )^2p_3+(1-alpha )^3p_4+cdots over 1+(1-alpha )+(1-alpha )^2+(1-alpha )^3+cdots
理論上這是一個无穷级数,但由於1-α少於1,各項的數值會越來越細,可以被忽略。分母方面,若有足夠多項,則其數值趨向1/α。即,
- EMA=α×(p1+(1−α)p2+(1−α)2p3+(1−α)3p4+⋯)displaystyle textEMA=alpha times left(p_1+(1-alpha )p_2+(1-alpha )^2p_3+(1-alpha )^3p_4+cdots right)
假設k項及以後的項被忽略,即α×((1−α)k+(1−α)k+1+⋯)displaystyle alpha times left((1-alpha )^k+(1-alpha )^k+1+cdots right)






其他加權
有時計算移動平均時會加入其他變數,例如,「交易量加權」會加入交易量的因素。
內部連結
- 技術分析
- K線
布林帶(BBands)
隨機指標(KD)
相對強弱指數(RSI)
指數平滑異同移動平均線(MACD)
乖離率(BIAS)
參考文献
^ NIST/SEMATECH e-Handbook of Statistical Methods: Single Exponential Smoothing,National Institute of Standards and Technology
外部連結
- Investopedia的介紹
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||









