Dyjtyuk

正八面體
(按這裡觀看旋轉模型)
類別	正多面体
面	8
邊	12
頂點	6
歐拉特徵數	F=8, E=12, V=6 (χ=2)
面的種類	正三角形
面的佈局（英语：Face configuration）	83
頂點圖	3.3.3.3
施萊夫利符號	3,4 and $beginBmatrix3\3endBmatrix$
對稱群	4
參考索引	U₀₅, C₁₇, W₂
對偶	正六面體
二面角	109.47122° = arccos(-1/3)
特性	正凸三角面多面體
3.3.3.3 （頂點圖）
(展開圖)
查论编

正八面體是一種八面體，由八個等邊三角形，分別為上、下各四個三角形與一個正方形組成的正方錐體，上下黏合在一起而構成，是五種正多面體的第三種，有6個頂點和12條邊。正八面體也是正三角反棱柱。正八面体是三维的正轴形，施莱夫利符号3,4，考克斯特—迪肯符号（英语：Coxeter-Dynkin diagram）。

正八面體每四条棱可以成为一个正方形，共有三个独立的正方形。

八面體

性質

頂點數目：6

邊數目：12

面數目：8

當邊長為a時：
- 表面積： $S=2sqrt 3a^2$
- 體積： $V=frac 13sqrt 2a^3$
- 外接球半径： $r_u=frac sqrt 22a$ （外接球即过正八面体各顶点的球）
- 内切球半径： $r_i=frac sqrt 66a$ （内切球即与正八面体各面相切的球）
- 中交球半径： $r_m=frac 12a$ （中交球即过正八面体各边中点的球）

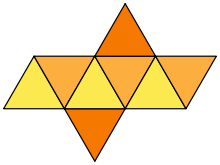
正八面体共有11种不同的展开图

坐标系

以棱长为√2的正八面体的几何中心作为原点，将正八面体的对角线作为x,y,z轴建立三维直角坐标系（正八面体的3条对角线两两正交，这也是正八面体被叫做“正轴形”的原因），则我们能将正八面体的顶点坐标记为

( ±1, 0, 0 )

( 0, ±1, 0 )

( 0, 0, ±1 )

正八面体表面方程为：
|x|+|y|+|z|=1

更一般的，如果正八面体的对角线平行于坐标轴，中心为(x₀,y₀,z₀)，外接圆半径为r（棱长为(√2)r），则正八面体表面方程为：
|x-x₀|+|y-y₀|+|z-z₀|=r

如果中心在原点的正八面体被拉长，成为菱形体，则更一般的八面体方程为
$left|frac xx_mright|+left|frac yy_mright|+left|frac zz_mright|=1$

其内接于椭球体
$frac x^2x_m^2+frac y^2y_m^2+frac z^2z_m^2=1$

表面积S和体积V为：
$S=4,x_m,y_m,z_mtimes sqrt frac 1x_m^2+frac 1y_m^2+frac 1z_m^2$
$V=frac 43,x_m,y_m,z_m$

它的惯性张量I是：

I=beginbmatrixfrac 110m(y_m^2+z_m^2)&0&0\0&frac 110m(x_m^2+z_m^2)&0\0&0&frac 110m(x_m^2+y_m^2)endbmatrix

当 $x_m=y_m=z_m=a,frac sqrt 22$ 时，菱形体为上述正八面体。

正交投影

正八面体可以以多种不同的方向被正交投影到二维平面，以下表格展示了几种特殊的投影：

正交投影
正对于	棱	面的平行方向	顶点	面
图像
投影对称性	[2]	[2]	[4] B₂	[6] A₂

对称性和表面涂色

正八面体作为3维的正轴体正多面体，自身拥有较高的对称性，它的所有面都是不可区分的。可是我们也可以想象将正八面体的面“涂上”不同的“颜色”，使它其的不同面拥有不同的“几何意义”，使正八面体拥有不同的对称性。正八面体的对称群是O_h（正八面体群），是三维的超正八面体群（英语：Hyperoctahedral group）。在此对称性下，正八面体的所有面都带有相同对“颜色”，对称性最高，群阶48。该群的子群体现了正八面体更低的对称性：T_d（群阶24），截半正四面体的对称群；D_3d（群阶12），三角反棱柱的对称群；D_4h（群阶16），四角双棱锥（正四棱柱的对偶）的对称群；D_2h（群阶8），三维长菱体（三维长方体的对偶）的对称群。

名称	正八面体	截半正四面体 (四面四面体)	正三反棱柱	正四双棱锥	长菱体
考克斯特符号（英语：Coxeter-Dynkin diagram）
施莱夫利符号	3,4	t₁3,3	h_0,12,6 s2,3	f_0,12,4 + 4	f_0,1,22,2 + +
Wythoff符号（英语：Wythoff symbol）	4 \| 3 2	2 \| 4 3	2 \| 6 2 \| 2 3 2
对称群（英语：List of spherical symmetry groups）	O_h, [4,3], (*432)	T_d, [3,3], (*332)	D_3d, [2⁺,6], (2*3) D₃, [2,3]⁺, (322)	D_4h, [2,4], (*422)	D_2h, [2,2], (*222)
对称群阶	48	24	12 6	16	8
图像 (半正表面涂色)	(1111)	(1212)	(1112)

與其他形狀的關係

对偶性

正八面體的對偶多面體是立方體。

當正八面體在立方體之內：

正八面體體積 : 立方體體積

=[(1/3)×高×底面積]×2 : 邊³

=(1/3)(n/2)[(n²)/2]2 : n³

=1 : 6

其它几何关联

正八面体即是星形八面体两正四面体的交集

两个互为对偶的正四面体可以组成一个复合正多面体，这两个正四面体的交集即是正八面体。这个复合多面体，也叫做星形八面体，是正八面体的第一个也是唯一一个星形展（英Stellation，暂译，目前还没有好的译名）。另一方面，从正四面体各棱中点处截去4个包含原顶点在内的线性大小只有原正四面体一半的正四面体，你也能得到正八面体，也就是说，正八面体是“截半正四面体”。在这里，正四面体与正八面体之间的关系就像立方体、正八面体与截半立方体；正十二面体、正二十面体与截半正十二面体一样。

除此以外，我们知道正二十面体还是“扭棱正四面体”，因此，正八面体与其也应该有关系。事实上，我们能够利用黄金分割从正八面体的棱上得到正二十面体的顶点。具体操作是：用有向线段代替这个正八面体的各棱，使每个面的3条有向线段恰好首尾相接，构成一圈。接着顺着每个有向线段的方向将其以黄金比例分割，分割点即是正二十面体的顶点。如果给定一正二十面体，则有5个不同的正八面体都可用上述操作得到给定正二十面体，这5个正八面体又可构成一复合正多面体，即五複合正八面體。

正八面体—正四面体堆砌的一部分

正八面体可以和正四面体一起完成三维空间的密铺，这密铺被叫做正八面体—正四面体堆砌(Octahedral-Tetrahedral Honeycomb)（同时它也是交错立方体堆砌(Alternated Cubic Honeycomb)，亦即半立方体堆砌(Demicubic Honeycomb)），是28个三维半正堆砌之一，是除立方体堆砌以外唯一一个完全由正多面体完成的三维堆砌。正八面体也参与了截半立方体堆砌。

正八面体是柏拉图立体中唯一一个在顶点处有偶数个面相交的，也是唯一一个所有对称镜面不穿过任何一面的。

以约翰逊多面体的角度来看，正八面体是双四棱锥，将其上下两个顶点截取，即得到双四棱台。

正八面体是四连通的，意味着要想打断正八面体6个顶点之间的连接，至少要撤掉4个顶点。它是4个四连通单纯形面全覆盖多面体之一，意味着它所有顶点的极大独立集（英语：maximal independent sets）都有相同大小。其余3个多面体是约翰逊多面体双五棱锥、变棱双五角锥和一个非半正的有12个顶点和20个正三角形面的多面体。

数学以外的正八面体

四面体桁架

巴克敏斯特·富勒在20世纪50年代发明了一种由正四面体和正八面体构成的球节架，其结构就是正八面体—正四面体堆砌，是公认的最强的抗悬臂压力的架结构。

四面体桁架，其中半个正八面体被加亮了

參見

八面體數

对称性: [4,3], (*432)							[4,3]⁺, (432)	[1⁺,4,3], (*332)	[4,3⁺], (3*2)


4,3	t_0,14,3	t₁4,3	t_1,24,3	3,4	t_0,24,3	t_0,1,24,3	s4,3	h4,3	h_1,24,3
半正多面体的对偶


V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3

对称性: [3,3], (*332)							[3,3]⁺, (332)


3,3	t_0,13,3	t₁3,3	t_1,23,3	t₂3,3	t_0,23,3	t_0,1,23,3	s3,3
半正多面体对偶


V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

搜尋此網誌

Dyjtyuk

正八面體

目录

性質

坐标系

正交投影

对称性和表面涂色

與其他形狀的關係

对偶性

其它几何关联

相关多面体

作为正八面体

作为截半正四面体

作为三角反棱柱

作为四角双棱锥

四面半六面体

数学以外的正八面体

四面体桁架

參見

Popular posts from this blog

【情報】本週珍珠商品重點：煉金時裝 + 艾港勞工宿舍！！

京昆高速公路

【攻略】陳戈-謝勒汗智慧的古書 (完成)

半正反棱柱
2	3	4	5	6	7	8	9	10	11	12	...


作为球面镶嵌

半正对偶双棱锥
2	3	4	5	6	7	8	9	10	11	12	...	∞


作为球面镶嵌