量子穿隧效應

量子穿隧效應示意圖。在粒子穿越高位勢壘阻礙的過程中,量子幅不會立刻變為零,而會呈指數衰變,因此,粒子抵達位勢壘的另一邊的概率也會降低。
在量子力學裏,量子穿隧效應(Quantum tunnelling effect)指的是,像电子等微观粒子能夠穿入或穿越位勢壘的量子行為,儘管位勢壘的高度大於粒子的總能量。在經典力學裏,這是不可能發生的,但使用量子力學理論卻可以給出合理解釋。[1]:xix
量子穿隧效應是太陽核聚變所倚賴的機制。量子穿隧效應限制了太陽燃燒的速率,是太陽聚變循環的瓶頸,因此維持太陽的長久壽命。[2]:625[3]許多現代器件的運作都倚賴這效應,例如,隧道二極管、場致發射、約瑟夫森結、磁隧道結等等。扫描隧道显微镜、原子鐘也應用到量子穿隧效應。[2]:257, 260, 437, 454量子穿隧理論也被應用在半導體物理學、超導體物理學等其它領域。
至2017年為止,由於對於量子穿隧效應在半導體、超導體等領域的研究或應用,已有5位物理學者獲得諾貝爾物理學獎。[4]
目录
1 歷史
2 入門概念
2.1 能量-時間不確定性原理
2.2 德布羅意假說
3 重要應用
3.1 恆星核聚變
3.2 放射性衰變
3.3 星際雲的天體化學
3.4 量子生物學
3.5 冷發射
3.6 隧道結
3.7 隧道二極管
3.8 扫描隧道显微镜
4 超光速穿隧
5 數學導引
6 參閱
7 參考文獻
歷史

弗里德里希·洪德
1927年,在研究分子光譜時,弗里德里希·洪德發現,對於雙阱位勢案例,偶對稱量子態與奇對稱量子態會因量子疊加形成非定常波包,其會從其中一個阱穿越過中間障礙到另外一個阱,然後又穿越回來,這樣往往返返的震盪。洪德定量給出震盪週期與位勢壘的高度、寬度之間的關係。[1]:4[5]
喬治·伽莫夫於1928年,發表論文用量子穿隧效應解釋原子核的阿爾法衰變。在經典力學裏,粒子會被牢牢地束縛於原子核內,因為粒子需要超強的能量才能逃出原子核的位勢。經典力學無法解釋阿爾法衰變。在量子力學裏,粒子不需要具有比位勢還強勁的能量,才能逃出原子核的束縛;粒子可以機率性的穿越過原子核的位勢,從而逃出原子核的束縛。伽莫夫想出原子核的位勢模型,其為吸引性核位勢與排斥性庫侖位勢共同形成。藉著這模型,他用薛丁格方程式推導出進行阿爾法衰變的放射性粒子的半衰期與能量的關係方程式,即蓋革-努塔爾定律。[1]:2
馬克斯·玻恩在一場伽莫夫的專題研討會裡,明白了伽莫夫理論的重要性,玻恩認為,這理論可能可以應用於其它領域,例如,電子從金屬表面冷發射的現象。玻恩是量子力學大師,他發現伽莫夫理論存在瑕疵﹐伽莫夫理論所使用的哈密頓量是厄米算符,其特徵值必須是實數,而不是伽莫夫所假定的複數。為此,經過幾個星期的努力,玻恩將這理論加以修改,並仍舊維持不變原先的結果。伽莫夫提出的阿爾法衰變機制是首次成功應用量子力學於核子現象的案例。[1]:2-3[6]:322-323
同時期,普林斯頓大學副教授羅納德·格尼閱讀了兩篇關於量子穿隧效應的論文。其中一篇的作者是罗伯特·奥本海默。在這篇論文裡,奥本海默將氫原子激發態的自電離歸因於量子穿隧效應,在原子裡,束縛電子的庫侖位勢阱被強勁電場改變,因此形成有限位勢壘,其可被電子穿越而過。[7]另一篇的作者是拉爾夫·福勒與羅特哈·諾德海姆。他們研究發現,一維量子系統具有某些很有意思的量子穿隧性質,可以用來解釋電子的冷發射,即施加強勁外電場於冷金屬可以促成電子被發射的現象。[7]早在1922年,朱利斯·利廉費德就已觀察到電子冷發射現象,但物理學者最初都無法對於這現象給出合理解釋。格尼認為,除了電子冷發射現象以外,量子穿隧效應也可以用來解釋阿爾法衰變。他找到欧内斯特·卢瑟福的學生,普林斯頓大學副教授愛德華·康登一起合作研究,很快地,他們也獨立地研究出阿爾法衰變的量子穿隧效應。[1]:3[8]
之後,兩組物理團隊分別繼續發表了一些關於量子穿隧效應的論文。伽莫夫的論文指出,低能量質子或阿爾法粒子可以穿越進入原子核,不管它們的能量是否高過位勢壘的高度。格尼的論文詳細地解釋了谐振隧穿的物理機制。1931年,華特·蕭特基給出德文術語「wellenmechanische Tunneleffekt」,即「波動力學穿隧效應」。隔年,雅科夫·弗伦克尔在著作《波動力學,基本理論》裡,首先給出英文術語「tunnel effect」。[4]在30年代與40年代,物理學者嘗試用電子穿隧機制來解釋在金屬半導體系統裡電子流的整流性質,但遭遇到很多困難,時常會得到相反的答案。直到1947年,由於發現電晶體,電子穿隧效應才又成為熱門研究論題。[1]:4
江崎玲於奈於1957年發明了隧道二極體,這器件展示出固體的電子穿隧性質。隧道二極體是首個被發明的量子電子器件。[9]3年後,伊瓦爾·賈埃弗做實驗證實在超導體裡也會出現量子穿隧效應,因此展示出超導體所具有的能隙,其為BCS理论的重要預測之一。1962年,布赖恩·约瑟夫森發佈理論預測,超電流可以穿越過在兩個超導體之間由一薄層絕緣氧化物製成的位勢障礙,约瑟夫森表示,這是因為成對電子(庫柏對)的穿越動作。[1]:4-5
由於江崎玲於奈與賈埃弗分別“发现半导体和超导体的隧道效应”,约瑟夫森“理论上预测出通过隧道势垒的超电流的性质,特别是那些通常被称为约瑟夫森效应的现象”,他們共同榮獲1973年諾貝爾物理學獎。[10]
扫描隧道显微镜是一种利用量子穿隧效應來探测物质表面结构的仪器。格尔德·宾宁及海因里希·罗雷尔於1981年在IBM的苏黎世实验室发明,两位发明者因此与恩斯特·鲁斯卡分享1986年诺贝尔物理学奖。[11]
水分子穿隧效應指的是,水分子陷俘在綠柱石內會穿隧於六種不同的旋轉取向,這意味著每一個水分子會同時處於六種組態。2016年,橡樹嶺國家實驗室研究團隊觀測到水分子穿隧效應。[12]
入門概念
微觀粒子穿越過一個位勢壘。粒子的能量在穿越前與穿越後維持不變,但量子幅會降低。
量子穿隧效應屬於量子力學的研究領域,量子力學研究在量子尺度所發生的事件。設想一個運動中的粒子遭遇到一個位勢壘,試圖從位勢壘的一邊(區域 A)移動到另一邊(區域 C),這可以被類比為一個圓球試圖滾動過一座小山。量子力學與經典力學對於這問題給出不同的解答。經典力學預測,假若粒子所具有的能量低於位勢壘的位勢,則這粒子絕對無法從區域 A移動到區域 C。量子力學不同地預測,這粒子可以概率性地從區域 A穿越到區域 C。[1]:9-10
能量-時間不確定性原理
初步看來,量子穿隧問題似乎是個佯謬,但是使用能量-時間不確定性原理可以合理解釋這問題。假設粒子的原本能量為Edisplaystyle E


ΔEΔt≈ℏ/2displaystyle Delta EDelta tapprox hbar /2;
其中,ΔEdisplaystyle Delta E


儘管在經典力學裡,總能量不能改變,否則,會違背能量守恆定律。然而,在量子力學裡,假若時間的不確定性為Δtdisplaystyle Delta t

現在,假設粒子暫時借得能量ΔEdisplaystyle Delta E




注意到兩點:
- 假若位勢壘過寬與過高,則粒子借得足夠能量在時間限制內從區域 A移動到區域 C是很困難的事件,這事件的概率會變得非常低,大多數粒子都會被反射回去。
- 按照上述解釋,由於粒子的能量變得大於位勢壘的位勢,粒子不是穿越過位勢壘,而是跳躍過位勢壘。
德布羅意假說

假設用手緊握一個裝有水的玻璃杯,則因為受抑全反射會使得指紋顯露出來。在玻璃杯表面與皮膚的凹凸紋之間有空氣間隙。假若間隙很淺薄,則光線會接觸到皮膚的凸紋並且反射出皮膚顏色;否則假若間隙很深厚,則光線會衰變,因此無法接觸到皮膚的凹紋,無法反射出皮膚顏色。[14]
根據德布羅意假說,微觀物質都具有波動性質,都會展示出像波動一般的物理性質。假若波動能夠展示出穿隧行為,則微觀粒子應該也可以展示出這種行為。例如,受抑全反射是一種波動穿隧行為,下面將詳細描述相關細節。[13]:75-76
假設光線從玻璃入射至空氣,由於光線的傳播速度在玻璃裡小於在空氣裡,所以在兩種不同介質的界面,會有一部份光線會被折射至空氣,其餘部分則會被反射回玻璃。但是,當入射角比臨界角大時(光線遠離法線的夾角),不會有任何光線被折射至空氣,所有光線都會反射回玻璃,這現象稱為全內反射。雖然沒有任何光線傳播進入空氣,但是,仍舊會有一種波擾動出現在空氣區域,這種波擾動稱為漸逝波,其振幅會隨著與界面的垂直距離呈指數衰減。
假設在與第一塊玻璃相離不遠之處置放第二塊玻璃,兩塊玻璃相互平行,在兩塊玻璃的中間是空氣區域,現在緩慢地將第二塊玻璃移向第一塊玻璃,直到漸逝波開始穿越到第二塊玻璃,這時,光線會傳播到第二塊玻璃,兩塊玻璃相離越近,越多光線會傳播到第二塊玻璃,光線的這種穿隧行為稱為受抑全反射。在現代光學裡分束器的運作就是倚賴受抑全反射的機制,通過調整間隔距離,可以操控分束器所反射或透射的光線數量。其它種波動也可以展示出類似受抑全反射的穿隧行為。藉著德布羅意假說,這種行為可以用來類比量子穿隧效應。
重要應用
恆星核聚變
在恆星裡發生的核聚變的關鍵機制是量子穿隧效應。恆星中心的溫度大約為107K,原子核的平均熱動能大約為1 keV。倘若要實現核聚變,原子核必須具有足夠能量來克服庫侖位勢壘,使得原子核與原子核之間的距離小於10-15 m,這能量大約為1 MeV,足足約為原子核平均熱動能的1000倍。因此,單獨熱動能並不能克服庫侖位勢壘來促成核聚變。儘管原子核的能量超小於庫侖位勢壘的位勢,量子穿隧效應仍舊能夠讓原子核穿越庫侖位勢壘,從而促成核聚變。[3]:第2節
在地球上,複雜的多細胞生命的演化有一個先決條件,即幾十億年長期穩定的太陽照射。在其它太陽照射的適居行星也可能需要這先決條件。到底是靠甚麼機制使得這麼長時間的穩定太陽照射成為可能?在太陽內部,最主要的反應是質子-質子反應,其穿隧概率大約為10-20,這給出跡象為什麼太陽能夠那麼長時期地靜燃燒氫原子(quiescent hydrogen burning)。然而,穿隧概率並不是反應概率(reaction probability),另外還有幾種關係到反應概率的重要因素,例如,貝塔衰變的速率。穿隧概率使得反應概率極度地與溫度有關,因此使得太陽內部的反應率變得很小,從而促成長時期地靜燃燒氫原子,這時期長達幾十億年,因此可以讓複雜的多細胞生命在地球進行演化。[3]:第2節
放射性衰變
放射性衰變是從不穩定的核素因為發射出輻射而變為其它種核素的過程,在這裡,輻射可以是粒子或電磁輻射。這過程的實現倚賴量子穿隧機制。伽莫夫提出的α衰变機制是首次成功應用量子力學於核子現象的案例。[6]:322-323
放射性衰變也是天體生物學的一個重要論題,因為放射性衰變能夠長期產生能量在適居帶以外的環境,其無法利用太陽照射來產生能量。例如,土衛二擁有活跃的地質,它很可能存在著生命,量子穿隧效在這裡扮演了很重要的角色。長期放射性核素,鈾-238、鈾-235與釷-232等等,通過α衰变給出放射熱,其能夠融化土衛二內部的冰結構,從而促使潮汐熱也能有效地產生作用,放射熱與潮汐熱共同使得這個小衛星擁有高度活耀的地質與水文。由此,人們認為,土衛二很可能隱藏著原始生命。[3]:第4節
地球有些不被太陽照射的區域仍舊能夠提供生物適居條件,α粒子穿隧機制在這裡扮演重要角色,例如,在深海裡,厭氧綠硫細菌利用地熱光來進行不產氧光合作用,地熱光是源自於高溫海底熱泉的熱輻射,而地球的熱通量大約有50%是源自於鈾-238與釷-232,這意味著地熱能的很大部分可以歸因於α粒子穿隧機制。在太陽系裡的各種天體的地表下面不被太陽照射的區域,由於α粒子穿隧機制提升溫度,很可能會隱藏著海洋。在化學演化、前生命化學、地外生物學等等學術領域,這論題相當有意思。[3]:第4節
星際雲的天體化學
在星系之間,星際雲的物質大多數是由氫氣與氦氣組成,其它最常見的元素有炭、氮、氧、鎂、鐵,大約為星際物質的0.1%。暗雲與中性瀰漫雲代表較冷的星際雲區域,溫度大約在10K至100K之間,由於內含灰塵的密度很高,大約為106原子每立方公分,電磁輻射無法傳播進入內部區域,溫度甚至可降低至30K。在冷星際雲裡,氫分子是豐度最高的分子,這揭示了一個長久未解的問題:由於氣態合成法的效率很低,以及紫外線與宇宙線的破壞,不應該會測量到那麼高豐度的氫分子。學者認為,氫原子被吸附在灰塵表面,在低溫時,移動性應該很低,很不容易與其它氫原子會合,從而形成氫分子,然而,通過量子穿隧機制,氫原子可以在灰塵表面擴散,有較高的移動性,因此能夠較容易地與另一個氫原子會合,從而形成氫分子。[3]:第3節
在星際雲裡,水分子、一氧化碳、甲醛與甲醇的合成,都需要用到量子穿隧機制,其可以促進在灰塵顆粒各種表面反應朝向重要前生命分子的合成。[3]:第3節
量子生物學
在量子生物學裡,量子穿隧效應是幾個重要的不平凡量子效應之一。對於許多生化學的氧化还原反应,例如,光合作用、細胞呼吸作用等等,電子的量子穿隧效應是關鍵因素。在DNA的自發性點突變裡,質子的量子穿隧效應是關鍵因素。[3]:第5節
佩尔-奥洛夫·勒夫丁首先給出,在雙螺旋裡由互變異構化引起的自發性點突變理論。他認為,質子可能會穿隧透過在DNA碱基对內的氫鍵的位勢壘,假設在質子穿隧之後,DNA又完成了複製的動作,則這整個過程被稱為自發性點突變。這過程意味著,質子的量子穿隧效應會影響DNA的主要功能,即基因信息的可靠儲存。[15]:850[3]:第5節
電子的量子穿隧機制是DNA能夠被修復的關鍵要素。紫外線照射會引起DNA鏈形成多個嘧啶二聚體,使得DNA遭到損害,DNA轉錄與DNA複製的功能被嚴重影響,甚至導致遺傳密碼被錯讀與突變。因紫外線照射產生反應,DNA鏈的相鄰嘧啶被二聚在一起。黄素蛋白光裂合酶能夠修補這種變樣的DNA。通過電子傳輸,連結嘧啶的共價鍵會被分裂,這樣,嘧啶二聚體得以變回先前的正常單體。在電子傳輸過程中,倚靠長距量子穿隧機制(最長距離約為3納米),電子才可從黄素部分移動至二聚體部分。總結,黄素蛋白光裂合酶之能夠修復被紫外線照射損害的DNA,完全是倚靠電子的長距量子穿隧機制。[3]:第5節[16]
冷發射
冷發射又稱為場致發射,即施加強勁外電場於金屬可以促成電子被發射的現象。用量子穿隧機制可以解釋這現象。從金屬表面需要做功才能提取電子,因此,電子在金屬內部的勢能大於在金屬外部。電子在金屬內部的物理行為可以簡單地用自由電子氣體模型來描述,在金屬內部,位勢為V(x)=0displaystyle V(x)=0


假設朝著金屬內部施加外電場Edisplaystyle mathcal E





|T¯|2=D0exp[−E0E]displaystyle;
其中,D0displaystyle D_0

在材料學裡,場致發射顯微鏡被用來觀測分子表面的結構與電子性質。[17]:135-181
隧道結

隧道結的示意圖:在導體A與B之間是絕緣體C,三者共同組成隧道結。
隧道結是由兩個導體與夾在它們中間的薄絕緣體所組成。根據經典電磁學的定律,電流無法通過絕緣體。然而,根據量子力學的定律,電子可以從任意一個導體通過絕緣體移動到另一個導體,這動作的概率大於零。假設施加偏壓,則會有電流從一個導體流動到另一個導體,而且,電流與偏壓遵守線性歐姆定律。這意味著隧道結的功能就如同電阻一般,而且電阻的電阻率不會隨時間而改變,電阻率與絕緣體厚度呈指數函數關係。通常,厚度大約為幾個奈米。[18]:287-289
假設兩個導體被改為超導體,則稱此隧道結為約瑟夫森結。庫柏對載著超導電流藉著量子穿隧效應流過絕緣體,這效應稱為約瑟夫森效應。在量子線路方面,約瑟夫森接面有許多重要的應用,例如超導量子干涉儀(SQUIDs)、超導量子計算以及快速單磁通量子(RSFQ)數位電子設備等。
隧道二極管

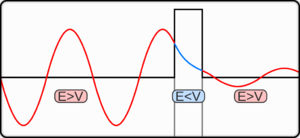
藍色實線、黑色虛線分別為隧道二極管、普通二極管的電流-偏壓曲線圖。
二極管是一種具有特定電流方向的半導體器件;施加同樣的電壓差,順方向的電流會比逆方向的電流大很多。在二極管的內部,P型半導體與N型半導體的接面區域被稱為耗盡層;在這區域內,電荷載子如P型半導體的受主與N型半導體的施主已幾乎被耗盡。耗盡層的物理行為主導了二極管的運作性質。假設P型半導體與N型半導體被高度摻雜,則耗盡層會變得非常狹窄,稍微施加順向偏壓,則電子可以很容易地從N型半導體的導帶穿隧通過耗盡層進入P型半導體的價帶,從而產生顯著的電流量。這種器件稱為隧道二極管。當N型半導體的導帶能級與P型半導體的價帶能級對齊時,電流量會達到最大值。這時,再增加順向偏壓會使得兩個能級不再對齊,這導致器件隨著順向偏壓的增加而變回為普通二極管。[19]:356-35
如右圖所示,在原點至點A之間,隨著增加順向偏壓V,穿隧電流I也會增加。點A是最大電流量點。在點A與點B之間,隨著增加順向偏壓,穿隧電流反而會遞減,隧道二極管的物理行為好似具有負值電阻。在點B右邊,可以忽略穿隧效應,隧道二极管的物理行為與普通二極管一般。[2]:453由於隨著偏壓的改變,穿隧電流也會迅速改變,穿隧二極管可以用來製作高速器件,開關頻率可達109Hz,普通半導體二極管的運作頻率遠低於這頻率。[19]:164-165
扫描隧道显微镜

扫描隧道显微镜描繪金屬表面特徵的工作示意圖。
扫描隧道显微镜可以展示出金屬的表面特徵,分辨率為原子尺寸的數量級。扫描隧道显微镜的操作原理主要是量子穿隧與距離之間的關係。如右圖所示,對於束縛在金屬內部的電子而言,扫描隧道显微镜的探測針與金屬表面之間的狹窄間隙扮演著位勢壘的角色,阻礙電子逃逸離開金屬表面,假設施加偏壓於探測針與表面之間,則會造成電子因穿隧效應從表面穿越位勢壘抵達探測針。穿隧電子所形成的穿隧電流能夠敏銳地反應出間隙距離的些微變化;稍微改變間隙距離0.5nm,就會改變穿隧電流104倍。因此,通過測量穿隧電流,可以估算探測針與表面之間的間隙距離。利用壓電反饋系統來改變探測針的位置,從而控制穿隧電流,維持穿隧電流與間隙距離都不改變,這樣,探測針的軌跡描繪出金屬樣品的表面特徵。[2]:257
超光速穿隧
多年來,對於粒子穿越位勢壘所需的間隔時間這論題,物理學者們爭執不休。簡略計算可以獲得超光速穿隧這理論結果,而近期一些實驗似乎也確切觀察到量子穿隧是一種超光速行為。但這不意味著信息傳播速度也可達超光速,因此並沒有違背狹義相對論的白紙黑字。[20]
理論分析量子穿隧時間是一門很複雜的學問。在量子力學裡,時間不是算符,而是參數,因此導致在對於測量兩個量子事件之間的間隔時間,能量-時間不確定性原理給出的意義不很明確。簡略地估算穿隧間隔時間ΔTdisplaystyle Delta T










- 這表達式的數值沒有上限,寬度越大,穿隧速度越大,甚至超過光速。
- 隨著增高位勢壘的高度Vdisplaystyle V
,穿隧間隔時間ΔTdisplaystyle Delta T
反而會減少;換句話說,阻礙的位勢越強勁,粒子的穿隧速度越快。
- 由於粒子借用能量的間隔時間ΔTdisplaystyle Delta T
與所借用的能量ΔEdisplaystyle Delta E
有關,與位勢壘的寬度無關,所以,不論位勢壘的寬度有多寬,粒子必須在間隔時間ΔTdisplaystyle Delta T
內穿越過位勢壘,否則,粒子無法穿越過位勢壘,量子穿隧效應不會發生。
上述分析相當簡略,然而當今一些更為詳細精緻的理論仍舊無法完全逃避推導出超光速穿隧這結果。量子穿隧是量子力學裡最奧妙的現象之一,為了要找到正確解答,必須進行更多嚴格研究。[20][5]
數學導引

對於一個不規則位勢壘的量子穿隧效應。往左與往右的量子波的波幅與方向都分別表示於圖內。入射波、反射波、透射波的波幅分別是Ardisplaystyle A_r,!
 、Aldisplaystyle A_l,!
、Aldisplaystyle A_l,! 、和Crdisplaystyle C_r,!
、和Crdisplaystyle C_r,! 。
。思考一個入射波Areikxdisplaystyle A_re^ikx,!






ψA(x)=Areikx+Ale−ikxdisplaystyle psi _A(x)=A_re^ikx+A_le^-ikx,!,
ψC(x)=Creikxdisplaystyle psi _C(x)=C_re^ikx,!。
而在位勢壘的內部,根據WKB近似,波函數大約為
ψB(x)≈Br|p|e−∫0x|p(x′)|dx′/ℏ+Bl|p|e∫0x|p(x′)|dx′/ℏdisplaystyle psi _B(x)approx frac B_rsqrt pe^dx'/hbar +frac B_lsqrt pe^int _0^x,!;
其中,p(x)=2m(E−V(x))displaystyle p(x)=sqrt 2m(E-V(x)),!
通過邊界條件的匹配,可以設定常數Aldisplaystyle A_l,!




一個粒子穿透過位勢壘的機率等於透射係數,定義為
T≡|Cr|2|Ar|2displaystyle Tequiv frac C_r,!。
假若位勢壘又寬又強,那麼,指數遞增項目必定很小,可以忽略。所以,
ψB(x)≈Br|p|e−∫0x|p(x′)|dx′/ℏdisplaystyle psi _B(x)approx frac B_rsqrt pe^dx'/hbar ,!。
毛估Crdisplaystyle C_r,!

|Cr||Ar|≈e−γ{displaystyle frac A_rapprox e^-gamma ,!;
其中,γ=∫0a|p(x′)|dx′/ℏdx'/hbar ,!
所以,粒子穿透過位勢壘的機率為
T=e−2γdisplaystyle T=e^-2gamma ,!。
請注意,取所有物理參數都超大於普朗克常數的經典極限,表達為ℏ→0displaystyle hbar rightarrow 0,!
參閱
- 超導量子干涉儀
參考文獻
^ 1.01.11.21.31.41.51.61.71.8 Razavy, Mohsen. Quantum Theory of Tunneling. World Scientific. 2003. ISBN 9812564888.
^ 2.02.12.22.3 Paul A. Tipler; Ralph Llewellyn. Modern Physics. W. H. Freeman. 2003. ISBN 978-0-7167-4345-3.
^ 3.03.13.23.33.43.53.63.73.83.9 Trixler, F. Quantum tunnelling to the origin and evolution of life. (PDF). Current Organic Chemistry. 2013, 17 (16): 1758–1770. PMC 3768233. PMID 24039543. doi:10.2174/13852728113179990083.
^ 4.04.1 Merzbacher, Eugene. The Early History of Quantum Tunneling. Physics Today. 2002, 55 (8): 44. doi:10.1063/1.1510281.
^ 5.05.1 Chiao, Raymond. Tunneling times and superluminality: a tutorial. AIP Conference Proceedings: 3–13. March 1999. doi:10.1063/1.57888.
^ 6.06.16.2 Griffiths, David J. Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. 2004. ISBN 978-0-13-805326-0.
^ 7.07.17.2 Esaki, Leo. Long Journey Into Tunneling. Nobelprize.org. Nobel Media.
^ Gurney, R. W.; Condon, E. U. Wave Mechanics and Radioactive Disintegration. Nature. 1928, 122 (3073): 439. Bibcode:1928Natur.122..439G. doi:10.1038/122439a0.
^ Leo Esaki - Biographical. Nobelprize.org. Nobel Media.
^ The Nobel Prize in Physics 1973. Nobelprize.org. Nobel Media.
^ The Nobel Prize in Physics 1986. Nobelprize.org. Nobel Media.
^ Kolesnikov 等. Quantum Tunneling of Water in Beryl: A New State of the Water Molecule. Physical Review Letters. 22 April 2016 [23 April 2016]. doi:10.1103/PhysRevLett.116.167802.
^ 13.013.1 Anthony J. G. Hey; Patrick Walters. The New Quantum Universe. Cambridge University Press. 23 October 2003: 73–. ISBN 978-0-521-56457-1.
^ Ehrlich, Robert. Why toast lands jelly-side down: zen and the art of physics demonstrations. Princeton, New Jersey, USA: Princeton University Press. 1997: 182. ISBN 0-691-02891-5. 使用|accessdate=需要含有|url=(帮助)
^ Matta, Cherif F. Quantum Biochemistry: Electronic Structure and Biological Activity. Weinheim: Wiley-VCH. 2014. ISBN 978-3-527-62922-0.
^ Sinha, Rajeshwar; Hader, Donat. UV-induced DNA damage and repair: a review. Photochemical & Photobiological Sciences. 2002, 1 (4): 225–236. doi:10.1039/B201230H.
^ Walter G. Berl. Physical Methods in Chemical Analysis. Elsevier. 22 October 2013. ISBN 978-1-4832-7440-9.
^ Kittel, Charles, Introduction to Solid State Physics 8th, USA: John Wiley & Sons, Inc., 2005, ISBN 978-0-471-41526-8
^ 19.019.1 Krane, Kenneth. Modern Physics. New York: John Wiley and Sons. 1983. ISBN 0-471-07963-4.
^ 20.020.120.2 Davies, P. C. W. Quantum tunneling time. American Journal of Physics. January 2005, 73 (1): 23–27. doi:10.1119/1.1810153.
| ||||||||||||||||||||||||||||||||||||||||||||||
|