Dyjtyuk

本条目部分链接不符合格式手冊規範。跨語言链接及章節標題等處的链接可能需要清理。（2015年12月12日） 請協助改善此條目。參見WP:LINKSTYLE、WP:MOSIW以了解細節。突出显示跨语言链接可以便于检查。

J₃₇：異相双四角台塔柱是唯一一個點正的：每個頂點都是三個正方形和一個等邊三角形。

J₉₂：三角廣底球形屋根丸塔是唯一一個擁有3,4,5,6邊形面的

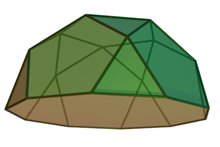
J₆：正五角丸塔，它是半正多面體截半二十面體的一半

J₅：正五角台塔

Johnson多面體，有譯作约翰逊多面体或莊遜多面體，是指正多面體、半正多面體、棱柱、反棱柱之外，所有由正多邊形面組成的凸多面體。這些立體由諾曼·詹森（英语：Norman Johnson (mathematician)）在1966年命名；1969年，維克托·查加勒（英语：Victor Zalgaller）證明只有92個這樣的立體。

• 因為在一個頂點相遇的面，每個面在該頂點的角的角度之和，不大於360°，又因為正多邊形的內角至少為60°，故每點最多有五個面在同一頂點。


• 所有Johnson多面體的面都是3, 4, 5, 6, 8或10邊形。

分類

Johnson多面體的構成方法之一是將其他由正多邊形面組成的凸多面體和下面幾種立體的拼合：

• 
  棱錐：以正三、四、五邊形為底而成的角錐。如：正四角錐（J₁）、正五角錐（J₂）


• 
  帳塔（平頂塔）：有兩個在空間中平行的正多邊形，其中一個的邊數是另一個的兩倍。在兩者間加入三角形和正方形。如：正三角帳塔(J₃)、正四角帳塔(J₄)、正五角台塔(J₅)。


• 
  罩帳：有兩個在空間中平行的正多邊形，其中一個的邊數是另一個的兩倍。在兩者間加入三角形和正五邊形。如：正五角罩帳(J₆)、正五角罩帳反角柱(J₂₅)。

另一種方法就是將這個凸多面體「切除」或「加上」一些立體。如：小斜方截半二十面體欠一側帳塔(J₇₆)。

有八個Johnson多面體不能以這些方法取得。如：球形屋根(J₈₆)及其它。

立體介紹

共有92種立體列於下表，表中J_n代表編號，V為頂點數，E為邊數，F為面數。

棱錐及塔

• 棱錐


• 台塔


• 丸塔

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
1	正四角錐		5	8	5	4	1					C4v
2	正五角錐		6	10	6	5		1				C5v
3	正三角台塔		9	15	8	4	3		1			C3v
4	正四角台塔		12	20	10	4	5			1		C4v
5	正五角台塔		15	25	12	5	5	1			1	C5v
6	正五角丸塔		20	35	17	10		6			1	C5v

錐柱及雙錐

• 錐柱


• 錐反角柱


• 雙錐


• 雙錐柱


• 雙反角錐柱

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
7	正三角錐柱		7	12	7	4	3					C3v
8	正四角錐柱		9	16	9	4	5					C4v
9	正五角錐柱		11	20	11	5	5	1				C5v
10	正四角錐反角柱		9	20	13	12	1					C4v
11	正五角錐反角柱		11	25	16	15		1				C5v
12	雙三角錐		5	9	6	6						D3h
13	雙五角錐		7	15	10	10						D5h
14	雙三角錐柱		8	15	9	6	3					D3h
15	雙四角錐柱		10	20	12	8	4					D4h
16	雙五角錐柱		12	25	15	10	5					D5h
17	雙四角錐反角柱		10	24	16	16						D4d

台塔柱及丸柱

• 帳塔柱


• 丸塔柱


• 台塔反角柱


• 丸塔反角柱


• 雙角柱


• 雙台塔


• 台塔丸塔


• 雙丸塔


• 雙台塔柱


• 台塔丸塔柱


• 雙丸塔柱


• 雙台塔反角柱


• 雙丸塔反角柱

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
18	正三角台塔柱		15	27	14	4	9		1			C3v
19	正四角台塔柱		20	36	18	4	13			1		C4v
20	正五角台塔柱		25	45	22	5	15	1			1	C5v
21	正五角丸塔柱		30	55	27	10	10	6			1	C5v
22	正三角台塔反角柱		15	33	20	16	3		1			C3v
23	正四角台塔反角柱		20	44	26	20	5			1		C4v
24	正五角台塔反角柱		25	55	32	25	5	1			1	C5v
25	正五角丸塔反角柱		30	65	37	30		6			1	C5v
26	異相雙三角柱		8	14	8	4	4					D2d
27	同相雙三角台塔		12	24	14	8	6					D3h
28	同相雙四角台塔		16	32	18	8	10					D4h
29	異相雙四角台塔		16	32	18	8	10					D4d
30	同相雙五角台塔		20	40	22	10	10	2				D5h
31	異相雙五角台塔		20	40	22	10	10	2				D5d
32	同相五角台塔丸塔		25	50	27	15	5	7				C5v
33	異相五角台塔丸塔		25	50	27	15	5	7				C5v
34	同相雙五角丸塔		30	60	32	20		12				D5h
35	同相雙三角台塔柱		18	36	20	8	12					D3h
36	異相雙三角台塔柱		18	36	20	8	12					D3d
37	異相双四角台塔柱		24	48	26	8	18					D4d
38	同相雙五角台塔柱		30	60	32	10	20	2				D5h
39	異相雙五角台塔柱		30	60	32	10	20	2				D5d
40	同相五角台塔丸塔柱		35	70	37	15	15	7				C5v
41	異相五角台塔丸塔柱		35	70	37	15	15	7				C5v
42	同相雙五角丸塔柱		40	80	42	20	10	12				D5h
43	異相雙五角丸塔柱		40	80	42	20	10	12				D5d
44	雙三角台塔反角柱		18	42	26	20	6					D3
45	雙四角台塔反角柱		24	56	34	24	10					D4
46	雙五角台塔反角柱		30	70	42	30	10	2				D5
47	五角台塔丸塔反角柱		35	80	47	35	5	7				C5
48	双五角丸塔反角柱		40	90	52	40		12				D5

側錐柱體

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
49	側錐三角柱		7	13	8	6	2					C2v
50	二側錐三角柱		8	17	11	10	1					C2v
51	三側錐三角柱		9	21	14	14						D3h
52	側錐五角柱		11	19	10	4	4	2				C2v
53	二側錐五角柱		12	23	13	8	3	2				C2v
54	側錐六角柱		13	22	11	4	5		2			C2v
55	雙側錐六角柱		14	26	14	8	4		2			D2h
56	二側錐六角柱		14	26	14	8	4		2			C2v
57	三側錐六角柱		15	30	17	12	3		2			D3h

側錐正多面體

• 側錐正多面體


• 正多面體欠側錐

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
58	側錐正十二面体		21	35	16	5		11				C5v
59	雙側錐正十二面体		22	40	20	10		10				D5d
60	二側錐正十二面体		22	40	20	10		10				C2v
61	三側錐正十二面体		23	45	24	15		9				C3v
62	正二十面體欠二側錐		10	20	12	10		2				C2v
63	正二十面體欠三側錐		9	15	8	5		3				C3v
64	側錐正二十面體欠三側錐		10	18	10	7		3				C3v

側台塔半正多面體

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
65	側台塔截角四面體		15	27	14	8	3		3			C3v
66	側台塔截角立方體		28	48	22	12	5			5		C4v
67	雙側台塔截角立方體		32	60	30	16	10			4		D4h
68	側台塔截角十二面體		65	105	42	25	5	1			11	C5v
69	雙側台塔截角十二面體		70	120	52	30	10	2			10	D5d
70	二側台塔截角十二面體		70	120	52	30	10	2			10	C2v
71	三側台塔截角十二面體		75	135	62	35	15	3			9	C3v
72	側台塔小斜方截半二十面體		60	120	62	20	30	12				C5v
73	雙側台塔小斜方截半二十面體		60	120	62	20	30	12				D5d
74	二側台塔小斜方截半二十面體		60	120	62	20	30	12				C2v
75	三側台塔小斜方截半二十面體		60	120	62	20	30	12				C3v
76	小斜方截半二十面體欠一側台塔		55	105	52	15	25	11			1	C5v
77	雙側台塔小斜方截半二十面體欠一側台塔		55	105	52	15	25	11			1	C5v
78	側台塔小斜方截半二十面體欠一側台塔		55	105	52	15	25	11			1	Cs
79	二側台塔小斜方截半二十面體欠一側台塔		55	105	52	15	25	11			1	Cs
80	小斜方截半二十面體欠雙側台塔		50	90	42	10	20	10			2	D5d
81	小斜方截半二十面體欠二側台塔		50	90	42	10	20	10			2	C2v
82	側台塔小斜方截半二十面體欠二側台塔		50	90	42	10	20	10			2	Cs
83	小斜方截半二十面體欠三側台塔		45	75	32	5	15	9			3	C3v

其它

此九個Johnson多面體不能以切除、增加角錐、台塔、丸塔等方法取得。本段有些立體尚未有中文譯名，故暫採日本譯名。

Jn	名稱	圖像	V	E	F	F3	F4	F5	F6	F8	F10	點群
84	變稜雙五角椎 (Siamese dodecahedron)		8	18	12	12						D2d
85	變稜四角反角柱 (Snub square antiprism)		16	40	26	24	2					D4d
86	球形屋根 (Sphenocorona)		10	22	14	12	2					C2v
87	側錐球形屋根 (Augmented sphenocorona)		11	26	17	16	1					Cs
88	加長型球形屋根 (Sphenomegacorona)		12	28	18	16	2					C2v
89	廣底加長型球形屋根 (Hebesphenomegacorona)		14	33	21	18	3					C2v
90	五角錐球形屋根 (Disphenocingulum)		16	38	24	20	4					D2d
91	雙新月雙丸塔 (Bilunabirotunda)		14	26	14	8	2	4				D2h
92	三角廣底球形屋根丸塔 (Riangular hebesphenorotunda)		18	36	20	13	3	3	1			C3v

參考資料

• 
  Norman Johnson（英语：Norman Johnson）, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.


• 
  Victor A. Zalgaller（英语：Victor Zalgaller）. Convex Polyhedra with Regular Faces. Consultants Bureau. 1969. No ISBN.  The first proof that there are only 92 Johnson solids.

外部連結

• Sylvain Gagnon之"Convex polyhedra with regular faces^{[永久失效連結]}", Structural Topology, No. 6, 1982, 83-95.


• Paper Models of Polyhedra


• George W. Hart描述之Johnson多面體
  


• 92種立體的圖片


• 埃里克·韦斯坦因. Johnson多面體. MathWorld. 


• Johnson多面體虛擬模型


• Magnetic Blocks之Educational toy system for making Johnson solids and other polyhedra
  


• Vladimir Bulatov之Johnson多面體的虛擬模型