Dyjtyuk

在代數拓撲中，基本群（或稱龐加萊群）是一個重要的同倫不變量。帶點拓撲空間的基本群是所有從該點出發的環路的同倫等價類，群運算由環路的銜接給出。

基本群能用以研究兩個空間是否同胚，也能分類一個連通空間的覆疊空間（至多差一個同構）。

基本群的推廣之一是同倫群。

直觀詮釋：二維環面的情形

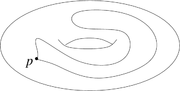
二維環面上由p點出發的環路

首先，讓我們考慮二維環面（或者可以想象成甜甜圈的表面）的例子作為熱身，固定其上一點pdisplaystyle p。

從此點出發，則可以建構環路（即：從pdisplaystyle p出發的並回到pdisplaystyle p的閉曲線）。設想環路如橡皮筋可自由變形與拉長，只要起點與終點仍是pdisplaystyle p 且環路仍處在環面上即可。這種變形叫做同倫，若一環路可以從另一環路藉此變形而得到，則稱兩者同倫等價。我們只探討環路的同倫類。二維環面的基本群由環路的同倫類組成。

a與b非同倫等價

在上圖中，adisplaystyle a與bdisplaystyle b並非同倫等價：無法連續地從一者變換到另一者而不將環路「扯斷」，它們代表基本群中的不同元素。藉著增加環繞圈數，可以獲得更多的同倫類。

a、b兩條環路的銜接

顧名思義，基本群不只是一個集合，它帶還有群結構：二元運算由環路的銜接給出，即先走完第一條環路，再走第二條環路，使得兩段環路上的速率相同。基本群中的單位元素ePdisplaystyle e_P由靜止在pdisplaystyle p點的環路代表，逆元由環路的逆行代表之，即：若一元素由環路s:[0,1]→T2displaystyle s:[0,1]to mathbb T ^2代表，則其逆元由s∘τ:[0,1]→T2displaystyle scirc tau :[0,1]to mathbb T ^2代表，其中τ(t)=1−t(t∈[0,1])displaystyle tau (t)=1-tquad (tin [0,1])。

形式定義

設Xdisplaystyle X為拓撲空間，pdisplaystyle p為其中定點。一條連續道路是一個連續映射γ:[0,1]→Xdisplaystyle gamma :[0,1]to X，而一個以pdisplaystyle p為基點的環路是一條滿足γ(0)=γ(1)=pdisplaystyle gamma (0)=gamma (1)=p的連續道路。以下若不另外說明，則環路皆以pdisplaystyle p為基點。

對兩條環路γ0,γ1displaystyle gamma _0,gamma _1，如果存在一個連續函數（保持基點的同倫）H:[0,1]2→Xdisplaystyle H:;[0,1]^2to X使得

• ∀t∈[0,1],H(t,0)=γ0(t)displaystyle forall tin [0,1],,H(t,0)=gamma _0(t)


• ∀t∈[0,1],H(t,1)=γ1(t)displaystyle forall tin [0,1],,H(t,1)=gamma _1(t)


• ∀x∈[0,1],H(0,x)=H(1,x)=pdisplaystyle forall xin [0,1],,H(0,x)=H(1,x)=p

則稱兩者同倫等價。不難驗證此關係確為等價關係。因此我們可考慮環路對此關係的等價類，以[γ]displaystyle [gamma ]表一環路γdisplaystyle gamma 隸屬的等價類，亦稱同倫類。

現在定兩條環路f,gdisplaystyle f,g的銜接為：
(f∗g)(t)={f(2t),t∈[0,1/2]g(2t−1),t∈[1/2,1]{displaystyle (f*g)(t)=leftbeginmatrixf(2t),&quad tin [0,1/2]\g(2t-1),&quad tin [1/2,1]endmatrixright.

直觀地說，此環路是先走fdisplaystyle f再走gdisplaystyle g，每一段都將速度加倍，以在單位時間內走完全程。可證明[f∗g]displaystyle [f*g]決定於[f],[g]displaystyle [f],[g]，因此可在環路的同倫類上定義二元運算「*」。不難看出此運算滿足結合律。

令單位元ePdisplaystyle e_P為環路eP(t)=pdisplaystyle e_P(t)=p（即靜止於pdisplaystyle p點的環路），並令環路f:[0,1]→Xdisplaystyle f:[0,1]to X之逆為f−1(t)=f(1−t)displaystyle f^-1(t)=f(1-t)（即fdisplaystyle f逆行）。可證明[f]↦[f−1]displaystyle [f]mapsto [f^-1]在同倫類上有明確定義，且同倫類在此運算下成為一個群。

此群稱為Xdisplaystyle X在基點pdisplaystyle p的基本群，表為π1(X,p)displaystyle pi _1(X,p)。

例子

• 
  Rndisplaystyle mathbb R ^n對任何基點的基本群皆為平凡群。換言之，每個環路都可以連續地變形到基點。這類空間稱為單連通空間。


• 當n≥2displaystyle ngeq 2時，Sndisplaystyle mathbb S ^n為單連通。


• 圓環S1displaystyle mathbb S ^1之基本群為Zdisplaystyle mathbb Z 。其元素一一對應於em:t↦e2iπmtdisplaystyle e_m:tmapsto e^2ipi mt，其中m∈Zdisplaystyle min mathbb Z 表示環路繞行圓環的次數（計入方向）；群運算由[em]⋅[en]=[em+n]displaystyle [e_m]cdot [e_n]=[e_m+n]給出。一般而言，ndisplaystyle n維環面的基本群同構於Zndisplaystyle mathbb Z ^n。


• 基本群也可能含撓元：例如射影平面RP2displaystyle mathbb R P^2的基本群便同構於Z/2Zdisplaystyle mathbb Z /2mathbb Z 。


• 基本群不一定可交換：例如挖去兩點的平面R2−a,bdisplaystyle mathbb R ^2-a,b的基本群同構於兩個生成元的自由群，生成元分別對應於繞行adisplaystyle a與bdisplaystyle b的環路。

事實上，可以證明對任何群Gdisplaystyle G皆存在一個拓撲空間，使其基本群同構於Gdisplaystyle G（此空間可以用二維CW複形構造，當群為有限展示時則能以四維流形構造）。

基本性質

對基點的獨立性

以下設Xdisplaystyle X為道路連通空間。p,q∈Xdisplaystyle p,qin X，則π1(X,p)displaystyle pi _1(X,p)同構於π1(X,q)displaystyle pi _1(X,q)。這是因為存在一條從pdisplaystyle p到qdisplaystyle q的道路γdisplaystyle gamma ，依之定義映射

[α]↦[γ]∗[α]∗[γ]−1displaystyle [alpha ]mapsto [gamma ]*[alpha ]*[gamma ]^-1

此映射給出從π1(X,q)displaystyle pi _1(X,q)至π1(X,p)displaystyle pi _1(X,p)的同構，其逆則為

[α]↦[γ]−1∗[α]∗[γ]displaystyle [alpha ]mapsto [gamma ]^-1*[alpha ]*[gamma ]

由此可談論空間本身的基本群（頂多差一個同構），記為π1(X)displaystyle pi _1(X)。基本廣群理論也'可以簡練地解釋基本群對基點的獨立性。

對連續映射的函子性

設fdisplaystyle f為空間(X,p)→(Y,q)displaystyle (X,p)to (Y,q)的同倫等價，則π1(f)displaystyle pi _1(f)為同構。

推論.同胚的空間有相同的基本群。

積空間的基本群

π1(X×Y,(p,q))=π1(X,p)×π1(Y,q)displaystyle pi _1(Xtimes Y,(p,q))=pi _1(X,p)times pi _1(Y,q)

與第一個同調群的關係

道路連通空間的第一個同調群是基本群的交換化。這是Hurwitz定理的特例。

計算方法與應用

范坎彭（van Kampen）定理

基本群一般不易計算，因為須證明某些環路非同倫等價。當空間可分割為較單純的空間，而其基本群已知時，范坎彭定理（或塞弗特－范坎彭（Seifert-van Kampen）定理）可以將基本群表為一個歸納極限。

錐定理與射影空間的基本群

對一個拓撲空間Xdisplaystyle X，定義其「錐」CX:=(I×X)/(0×X)displaystyle CX:=(Itimes X)/(0times X)，其中Idisplaystyle I表閉區間[0,1]displaystyle [0,1]。當X=S1displaystyle X=mathbb S ^1時，CXdisplaystyle CX同胚於圓錐。

道路連通空間的錐是單連通的，我們也有自然包含映射X≃1×X⊂CXdisplaystyle Xsimeq 1times Xsubset CX。

設f:X→Ydisplaystyle f:Xto Y為連續映射，定義映射錐為

C(f):=C(X)⊔Y[1,x]∼f(x)displaystyle C(f):=dfrac C(X)sqcup Y[1,x]sim f(x)。

例子：設fdisplaystyle f為S1displaystyle mathbb S ^1到自身的映射z↦z2displaystyle zmapsto z^2，此時C(f)=RP2displaystyle C(f)=mathbb R P^2。

錐定理斷言C(f)displaystyle C(f)的基本群同構於π1(Y)displaystyle pi _1(Y)對f∗(π1(Y))displaystyle f_*(pi _1(Y))的正規化的商

應用：實射影空間之基本群同構於Z/2Zdisplaystyle mathbb Z /2mathbb Z 。

圖、曲面與多面體的基本群

• 
  圖的基本群總是自由群。這點可藉著將圖沿其最小生成樹縮為一束S1displaystyle mathbb S ^1看出。


• 
  多面體的基本群可以展示為生成元與關係，使得每個關係由多面體的一個面給出。


• 可定向緊曲面的基本群帶一個有2gdisplaystyle 2g個生成元a1,b1,…,ag,bgdisplaystyle a_1,b_1,ldots ,a_g,b_g及一個關係a1b1a1−1b1−1a2b2a2−1b2−1…agbgag−1bg−1=1displaystyle a_1b_1a_1^-1b_1^-1a_2b_2a_2^-1b_2^-1ldots a_gb_ga_g^-1b_g^-1=1的展示。整數gdisplaystyle g決定於曲面的拓撲結構，稱為其虧格。

基本群與覆疊空間

基本群的子群的共軛類一一對應於空間的覆疊的同構類，在此對應下，正規子群對應於伽羅瓦覆疊。

在覆疊空間理論中，業已證明了如果空間有單連通的覆疊空間（例如對局部單連通空間），則基本群同構於萬有覆疊空間的自同構群。

推廣

基本廣群

如果一個小範疇（即：對象與全體態射構成一集合）的所有態射皆可逆，則稱之為一個廣群。所有廣群與其間的函子構成一個範疇。群是只有一個對象的廣群。

設Gdisplaystyle G為一廣群，對其對象定義下述等價關係：

x∼y⟺Hom(x,y)≠∅displaystyle xsim ,yiff mathrm Hom (x,y)neq emptyset

得到的商集記作π0(G)displaystyle pi _0(G)（或曰連通分支），這是從廣群範疇到集合範疇的函子。

對每個拓撲空間，以下述方式函子地構造一廣群πXdisplaystyle pi X：

設Xdisplaystyle X為拓撲空間，令πXdisplaystyle pi X的對象為Xdisplaystyle X的點，從點xdisplaystyle x至ydisplaystyle y的態射是從xdisplaystyle x到ydisplaystyle y的道路的同倫類。同倫等價關係相容於道路的頭尾相接，故定義了一個廣群πXdisplaystyle pi X，稱為Xdisplaystyle X的基本廣群。

Van Kampen定理在廣群的框架下有簡練的表述。

設Gdisplaystyle G為廣群，而xdisplaystyle x為其對象（也稱作Gdisplaystyle G的點）。Hom(x,x)displaystyle mathrm Hom (x,x)在態射合成下成為一個群，記之為π1(G,x)displaystyle pi _1(G,x)。註：由於基點選取問題，π1displaystyle pi _1並不能定義一個從廣群範疇到群範疇的函子。

一個拓撲空間的基本群可以用基本廣群定義為π1(X,x0):=π1(πX,x0)displaystyle pi _1(X,x_0):=pi _1(pi X,x_0)。

高階同倫群

基本群實則是第一個同倫群，這是符號π1(X,x0)displaystyle pi _1(X,x_0)中「1」的由來。

代數幾何中的基本群

基本群亦可抽象地定義為纖維函子的自同構群，此纖維函子對每個帶基點的覆疊映射r:(Y,q)→(X,p)displaystyle r:(Y,q)to (X,p)給出纖維r−1(p)displaystyle r^-1(p)。

此定義可以推廣到代數幾何，而之前給出的環路定義則不可。在此我們將拓撲空間的覆疊映射代為平展態射，拓撲空間的基點代為概形上的一個幾何點xdisplaystyle x，而纖維函子Fdisplaystyle F對一平展覆疊f:Y→Xdisplaystyle f:Yto X給出幾何纖維HomX(x,Y)displaystyle mathrm Hom _X(x,Y)。此推廣源出格羅滕迪克與夏瓦雷。

這套理論可以解釋函數域的伽羅瓦理論與黎曼曲面的覆疊理論之聯繫。

文獻

• Allen Hatcher, Algebraic Topology (2001), Cambridge University Press. ISBN 0521795400
  


• J. P. May, A Concise Course in Algebraic Topology (1999), Chicago University Press. ISBN 0226511839
  

外部連結

• Allen Hatcher, Algebraic Topology自由下載


• 基本群動畫展示