群同態
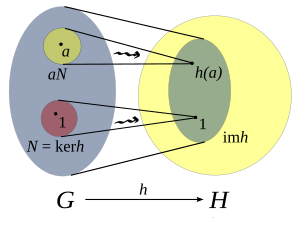
從G(左)到H(右)的群同態(h)的像。在H內的小橢圓形是h的像。N是h的核而aN是h的陪集。
在數學中,給定兩個群(G, *)和(H,·),從 (G, *)到 (H,·)的群同態是函數h : G → H使得對於所有G中的u和v下述等式成立
h(u * v) = h(u)·h(v)
在這裡,等號左側的群運算*,是G中的運算;而右側的運算·是H中的運算。
從這個性質,可推導出h將G的單位元eG映射到H的單位元eH,并且它還在h(u-1) = h(u)-1的意義上映射逆元到逆元。因此我們可以說h“兼容於群結構”。
更老的給同態h(x)的符號是xh,它容易混淆於索引或一般下標。更新近的傾向是把群同態寫在它們的自變量的右側,省略括號,如此h(x)簡化成了x h。這種方法特別流行於自動機扮演角色的群論領域,因為它更適應自動機從左至右讀字詞的習慣。
在考慮配備了加法結構的群的數學領域中,同態有時關照的不只是(如上)群結構而且還有額外的結構。比如拓撲群的同態經常要求是連續性的。
目录
1 像和核
2 例子
3 群範疇
4 同態映射的類型
5 阿貝爾群的同態
6 參見
7 引用
8 外部連結
像和核
我們定義h的核為被映射到H中單位元上的G中的那些元素的集合
- ker(h) = u ∈ G : h(u) = eH
定義h的像為
- im(h) = h(u) : u ∈ G 。
核是G的正規子群(事實上,h(g-1u g)= h(g)-1h(u) h(g) = h(g)-1eH h(g) =
h(g)-1h(g) = eH)而像是H的子群。同態h是單射(并叫做单同態)當且僅當ker(h) = eG。
同態的核和像可以被解釋為對它接近於同構程度的程度。第一同構定理聲稱群同態的像im(h)同構於商群G/ker(h)。
例子
- 考慮帶有加法的循環群Z/3Z = 0, 1, 2和整數集Z的群。映射h : Z → Z/3Z,有著h(u) = u 模以3,是群同態。它是滿射并且它的核由被三整除的所有整數構成。
指數映射產生從帶有加法的實數集R的群到帶有乘法的非零實數集R*的群的群同態。核是0而像由正實數組成。
- 指數映射還產生從帶有加法的複數集C的群到帶有乘法的非零複數集C*的群的同態。這個映射是滿射并且有核 2πki : k ∈ Z ,這可以從歐拉公式得出。
- 給定任何兩個群G和H,映射h : G → H,把所有G的元素對應到H的單位元,是同態;它的核是集合G。
- 給定任何群G,恒等映射id : G → G,有著id(u) = u對於所有G中的u,是群同態。
群範疇
如果h : G → H和k : H → K是群同態,則h o k : G → K也是群同態。這證明所有群的類,和群同態作為態射一起形成一個範疇。
同態映射的類型
如果同態h是雙射,則你還可以證明它的逆映射仍是同態,這種h叫做群同構;在這種情況下,群G和H被稱為是“同構的”:它們只在元素的符號上有差異而對於所有實踐用途都是同一的。
如果h: G → G是群同態,我們稱之為G的自同態。如果它進一步的是雙射并且因此是同構,則稱為同構。群G的所有自同構的集合,帶有函數復合作為運算,自身形成一個群,叫做G的自同構群。它指示為Aut(G)。作為例子,(Z, +)的自同構群只有兩個元素,恒等變換和乘以 -1;它同構於Z/2Z。
滿同態是滿射同態,單同態是單射同態。
阿貝爾群的同態
如果G和H是阿貝爾群(就是交換群),則所有從G到H的群同態的集合Hom(G, H)自身是阿貝爾群:兩個同態的和h + k定義為
- (h + k)(u) = h(u) + k(u),對於所有G中u。
H的交換律對于證明h + k也是群同態是必需的。同態的加法在如下意義上兼容於同態的復合:如果f在Hom(K, G)中,h, k是Hom(G, H)的元素,并且g在Hom(H,L)中,則
- (h + k) o f = (h o f) + (k o f),并且g o (h + k) = (g o h) + (g o k)。
這證明了一個阿貝爾群的所有自同態的集合End(G)形成了一個環,即G的自同態環。例如,由Z/2Z的兩個復本的直積構成的阿貝爾群(克萊因四元群)的自同態群同構於帶有Z/2Z內元素的2×2 矩陣的環。上述兼容性還證明所有阿貝爾群帶有群同態的範疇形成了預加法範疇;直積和良好定義的核的存在性使這個範疇成為阿貝爾範疇的原型例子。
參見
- 同態基本定理
引用
Lang, Serge, Algebra, Graduate Texts in Mathematics 211 3rd, Springer-Verlag, 2002 .
外部連結
PlanetMath上Group Homomorphism的資料。
| ||||||||||||||||||||||||||||||||||||||||||||
